EXAMPLES AUDIO

Content

Examples of use of the functions audio and of visualization and real time processings.

Key words

analog, real time.

Files MUSTIG

ACQUIS.MTG, GENESIG.MTG, FILTR_RII.MTG,  FILTR_RIF.MTG, in the directory “ACQUIS”

Related commented examples

Filtering, Spectral Analysis, RIF Filtering,  Convolution by TFD.

Acquisition of signal

Size of the acquisition buffers

The buffer of acquisition in input is a zone of memory where are memorized the samples acquired (to the rhythm of the acquisition frequency) before being treated (read by blocks by one of the ADC modules " 2 Channels " or " ADC nChannels "). In the cases of regular processing, it is sufficient that this buffer is of size a little superior to the size of the blocks multiplied by the number of channels. A good security is to raise it by a factor two. In the case of processing to variable duration (typically writing results on files on disk) it will be necessary to increase the size considerably.

The only inconvenience to overdimension the buffers of input is to reserve the memory.

The buffer of acquisition in output operates in an analogous manner. On the other hand, it is advised not to overdimensionner this buffer, because this creates a delay proportional to the size of the buffer.

Acquisition of only one block

The graph below achieves the acquisition and the visualization of a signal block. The macro “Init Acq” (constructed with the module “ADinit”) fixes the frequency of sampling and the size of the buffer zones (“buffers”). These zones must be dimensioned to a size larger than the product of the size of the blocks acquired by the number of channels. Here, the analog output not being used, the size of the output buffer is fixed to a very small value (a nul value is not allowed).

The macro “Init Acq” provides the frequency of sampling (that is the frequency, feasible by the card, the closest to the wished frequency), in kilohertz. This value is converted in second to fix the step of the variable “t.”

The module “ADC2Channels” achieves the acquisition and the numeric conversion of an analog signal block, on two channels. One here only views it.

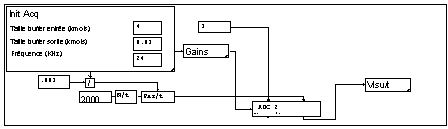
One notes that if one asks the calculation of the curve visualized, a new acquisition is achieved. In the same way, if one adds a processing, the acquisition will be redone. This working, that can seem abnormal to an accustomed of Mustig, is more convenient in a lot of cases. If one wants to analyze a transient, one will be able to record it in a file (by replacing the “View” by one macro of file writing), and to reread this file to treat it.

Continuous acquisition of blocks

One achieves here an infinite set of acquisition of blocks that are visualized progressively. It achieves a function analogous to the one of an oscilloscope.

To achieve this continuous acquisition, it is sufficient in a MUSTIG packet to loop the two pins input and output “synchro” of the module  “ADC2Channels.” (These pins of “synchro” don't transport any real information, but serve to specify only that the acquisitions of blocks are made one after the other.)

One then gets the macro “Acq_2/t/x” in the library “Bib_audio.”

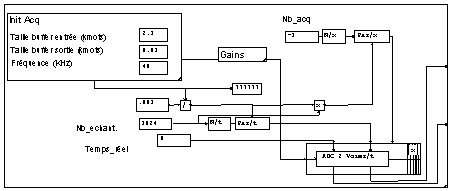
One will notice, in the parameters of this macro, that one put the flag “Real Time” to “0.” Indeed, for a simple visualization of signal, it is not bothersome to lose some samples between the blocks. (With an analog oscilloscope, the signal is always lost during the return of sweep). Consequently, the size of the necessary buffer is again the product of the size of the blocks acquired by the number of channels.

In output, one has a signal constituted of blocks function of the variable “t”, and indexed by the variable “x.” It is analogous to the output of a macro of reading of a disk file by blocks.

To achieve the visualization, one uses the macro “Animated View” (That is in “Outputs”). It is made from the macro “View” standard, completed by one macro “Slide” . This last achieves the display to the screen then the erasing of the successive visualizations .

Recording on disk

To achieve recording of an analog signal into a disk file, plug a macro “Ecriture2D/t/x"  behind the macro “Acq_2/t/x.”

In this case, it is imperative to put the flag "Real Time” to “1” not to risk to lose samples. It will be also useful to fix the size of the input buffer to a value equal to several times the size of the blocks. Indeed, the duration of writing of a block on disk is not regular. A sufficiently big buffer is necessary therefore to level these irregularities. There is not any inconvenience to put a very large size, provided that it holds in the memory of the card. (So much that the message “data memory saturated" doesn't appear).

Spectrum analyzor

The following graph achieves the acquisition of a signal, its spectral analysis and the visualization of this one.

The macro “SpectrumTR” is a modification of the macro “Spectrum” contained in the library “Processing Tools”, and described in the commented example “Spectral Analysis.” The sum on all blocks has been replaced by a low pass filter of the first order: one achieves then a spectral analysis with exponential average. The constant of time of this filter, expressed in blocks, is easily accessible.

Let's note that the macro “SpectrumTR” calculates the Fourier transform on blocks constituted of two blocks of input coupled (what comes back to use the blocks riding by halves). Consequently, it is important not to lose any information between the blocks acquired and therefore to put the flag “Real Time” to “1.” The size of the buffers should be fixed then at 2 times the product of the size of the blocks acquired by the number of channels.

One notes then on most machines that the working in real time is not possible to the maximum sampling frequency (48KHz). This is due to an insufficient drawing speed (the drawing is done by the PC). To hold the cadence, it is not necessary to do a drawing of every block.

A first solution would be to make the acquisition of a lot larger blocks (attention to dimension the buffers of acquisition consequently!), then to cut the blocks into sub- blocks and to visualize only the analysis averaged on these blocks. The macro “Spectrum” in Library can be parametered to do this cut.

Another solution, a few more flexible and less gluttonous in memory requires a modification of the macro “AcQ_2/t/x” in one macro “Acq_2b/t/b/x". It contains a duplicate packet around the "ADC2Channels" module. The signal of output is then a set of “blocks of blocks” indexed by “x”, the elementary blocks being indexed by “b.” The output of this macro is identical to the one of the module “Split” of the previous solution. The  same macro “Spectrum” in Library is used, but it doesn't make the cut.

Generation of signals

One is interested here in creating a sinusoid signal of given frequency and to send it on an analog output.

Generation of only one block

The following graph seems to fill the wanted function.

One uses one macro “AcqRest_2/t/x”, that can achieve at a time the acquisition (Digital Analog Conversion) and the restitution (Analog Digital conversion) of the signal. One doesn't use in fact the acquired values, but only their support, dimensioned in number of points and sampling rate inside the macro. The value of the frequency in the macro “Sine/t” is then in Hertz.

In fact, this graph is not satisfactory, because the phase of the sine is reset at every block. The result is only correct for the values of frequencies giving a whole number of periods by blocks. (In fact, the sine will be calculated only one time, which is economic when the result is satisfactory).

Generation by blocks of a continuous signal

To suppress the discontinuities of phase, it is necessary to calculate the phase of the first point of a block according to the one of the last point of the previous block. It is achieved easily by adding a second bundle, according to the variable “b” that indexes the blocks, in the calculation of the phase, inside the macro “sine”

     = >  

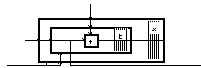
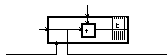Let's note that the generator of sine of the library uses a calculation of phase in whole arithmetic. It permits to get a calculation merely “modulo 2À.” A calculation in floating point without any precaution is unusable in real time: the calculation of the sine becomes less and less precise as the phase increases.

It is necessary to put the flag “Real Time” to “1” . The size of the output buffer will be fixed at 2 times the product of the size of the blocks acquired by the number of channels. It permits to calculate the following block while the current block is converted. Attention, contrary to the buffer of input, it is not desirable to increase the buffer of output uselessly: it increases the delay.

One will probably note that the maximum frequency is not reached: the calculation of the sine is relatively slow. The use of a table would be more efficient.

Generator of signals

The macro generating signals is comparable to a device “generator of function". It doesn't possess any output: its output is analog. The contents of the library macros “Sinus/t”, Carré_p/t”, Triangle_p/t” have been unified. A box of choice permits to direct one or the other of the three outputs.

FILTERINGS  RII

In the two following examples, one does a digital filtering on a signal that comes from the conversion of an analog signal, and one reconverts in analog the output of the numeric filter. One gets the equivalent of an analog filter globally.

The following graph seems to fill the wanted requirements. In fact, it is not satisfactory, because the filter is reset at every beginning of block. It results in picks at every passage from a block to another.

Two solutions exist. The first consists in transforming the vectorial function of acquisition in a scalar function, by using blocks of size 1. It is an easy solution to put in work, but it only functions at relatively low frequency.

The second solution is to replace all macros “Delay/t” of the filter by the macro “Delay_bc/t/x”(disponible in Library). Thanks to a duplicate bundle, this macro puts in first sample of an output block, the last sample of the input precedent block (See commentary of the examples “recursive filter”).

One will notice in these examples the use of the jump modules to get a linear graph. Otherwise, it appears looped by the fact that the converters of input and output are in the same macro. One will also notice that one connected the acquired signal directly on an input of the macro “AcqRest”, therefore on an analog output. It permits to measure the delay due to the filters of the converters and to the buffer memories, and by difference, the delay due to the digital filter.

In all applications of filtering, it is counseled to adjust the size of the output buffer to the necessary minimum not to increase uselessly the delay.

FILTERINGS  RIF

To achieve a filter at finite memory, it is possible to describe the filter by its diagram of flux. It will be necessary then as previously to replace the “Delay/t” by “Delay_bc/t/x.”

 The better solution will be generallyto do filtering with the help of the DFT. The macro “Filtering by parts” achieves a continuous filtering from a signal cut in blocks, as the one that comes out from the macro of acquisition.

One gives various examples of impulse response of filters.