Multi - Cadence filtering
Content
Filtering with sampling frequency change
Key words
interpolation, under - sampling, decimation, over sampling, filtering, multicadence
MUSTIG Files
Related commented examples
Interpolation, Interpolation by DFT
Theoretical principles
Decimation by an integer factor
The reduction of sampling frequency is often called " decimation ". If the reduction ratio is an integer number " k ", this operation comes back to keeping one sample only among k. But to be certain to respect the Shannon conditions of sampling, one must do a low-pass filtering previously (for the same reason, one must place a low-pass " anti - aliasing " filter on a continuous signal before its sampling). If this low-pass filter is achieved by a filter of finite impulse response of transverse type, the decimation is achieved by the following diagram:
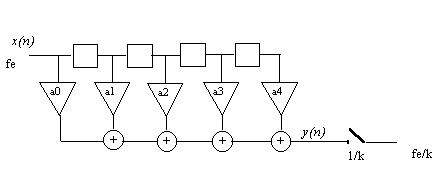
In fact, it is useless to calculate the outpit samples not used:
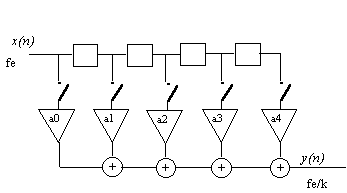
This structure is more economic in calculation.
Interpolation by an integer factor
The increase in the sampling frequency by an integer factor " p " can be made by inserting p-1 null values after every sample, then filtering with a low- pass filter to suppress the duplicated spectra :
In fact, one notes that only 1/p of the multiplieurs of the transverse filter operate on not null data. It is more economic in calculation to consider that to every sample correspond successively the different outputs of p filters operating on the samples of input. One gets a structure known as polyphase filter.
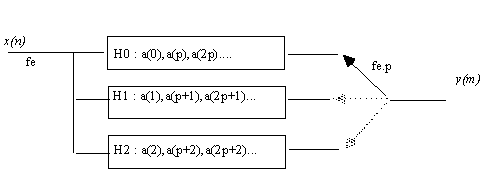
The I R.of the Hi filters are obtained by samplings from the I.R. of the low pass working at the high sampling frequency.
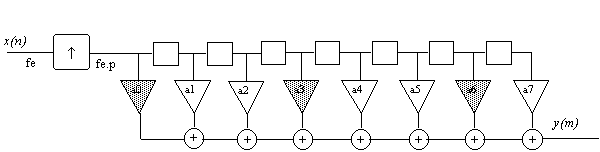
Décimator with fractional factor
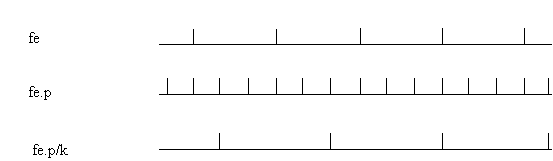
To pass from the sampling frequency fe to the sampling frequency fe. (p/k), one could first of all make an increase of the frequency to get fe.p, then a decimation in a k ratio. It is not necessary to add a low-pass before the decimation since the one of the interpolator already exists. It is sufficient therefore to under sample the output of the preceding polyphase filter.
In fact, it is not necessary to calculate the filters whose outputs are unused. The filter can be described then by the following digramme:
It is possible to use this structure in the case of an any output rhythm, by approximating the output sample to the value of the clock nearest fe.p.
MUSTIG realization
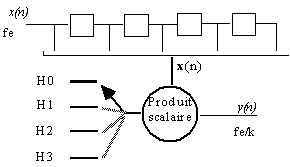
The examples of realization presented here use the vectorial operators of under - sampling available in MUSTIG. It restricts their use to signals either of limited length or cut into blocks. In the next versions, some scalar operators will permit more complete real time working.
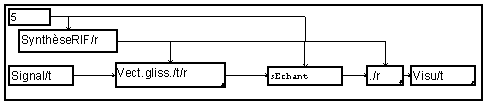
Decimation by an integer factor
While describing the transverse filter with the help of one macro " Sliding Vector " and of one macro " scalar product ", one gets the starting diagram:
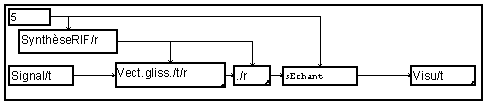
One verifies that it is equivalent (but faster!) to place the module of under - sampling before the scalar product :
The macro " FIR Synthesis " calculates the coefficients of a low-pass filter according to the under - sampling ratio given as a parameter.
Interpolation by an integer factor
One can verify the working of the elementary method easily: inserting zeros and filtering. The null value insertion is achieved by the macro " Suréchantillonne_0" (see commented example " Interpolation "). The amplitude of the signal is multiplied by the " p " factor of oversampling to preserve the power of the signal.
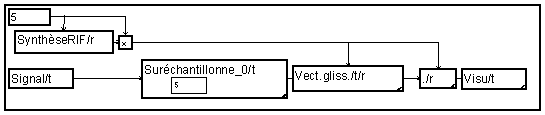
To transform this graph into a polyphase filter, one decomposes the impulse response into a set of p responses by the " Demultiplex " macro.
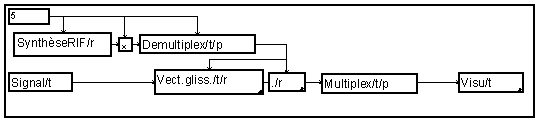
At the output of the filter, one has therefore a set of signals it is enough to multiplex to get the over - sampled signal.
Decimation by a fractional factor
We suppose that we well achieve a reduction of sampling frequency, that is to say that the ratio k/p is lower than 1. In this case, we have at most one sample of output in every period of the input signal.

The macro " Clock " builds a logical signal that indicates if there is a sample of output corresponding to the sample of input. This signal is applied as a validation signal to the " S_ECH " macro. This one keeps only the valid samples . Furthermore, the macro " Clock " calculates the position of the output sample relative to the input sample. This position is used to choose, by the module " cut ", the set of coefficients needed to calculate this sample.
By using this same macro " clock ", one can easily achieve frequency changers without interpolation or with a simple linear interpolation. By observing the spectra of the output signals, one notes that these simple structures have parasitic lobes, whereas the structure with interpolation by polyphase filter do not have.