Introduction 5
1.1 Généralités 55
1.3 Contenu de la livraison 5
2 Structure générale 5
2.1 Signal binaire 5
2.2 Formation des symboles 5
2.3 Modulation 5
2.4 Canal de transmission 6
2.5 Démodulation 6
2.6 Egalisation 6
2.7 Décision sur les symboles 6
2.8 Générateurs de fréquence 6
2.9 Visualisation et mesure 6
2.10 Remarques 6
3 Exemples de mise en œuvre 6
3.1 Codage 6
3.2 Principales méthodes de modulation (amplitude, phase) 8
3.2.1 Mise en forme par impulsions rectangulaires 8
3.2.2 Mise en forme par impulsions "racine de Nyquist" 9
3.2.3 Modulation-Démodulation non cohérente 10
3.2.4 Modulation-Démodulation cohérente 10
3.3 De la modulation PSK à la modulation GMSK 11
3.3.1 Modulation QPSK4 11
3.3.2 Modulation GMSK 13
3.4 Egaliseur de lignes de transmission 14
3.4.1 Egaliseur transversal 14
3.4.2 Egaliseur de Viterbi 15
3.5 Modulation multifréquence (DMT ou OFDM) 16
3.5.1 Etalement de spectre (CDMA) 16
3.5.2 Modulation multifréquence 17
3.6 Synchronisation 19
4 Descriptions détaillées 20
4.1 Signal binaire 20
4.2 Formation des symboles 20
4.3 Modulation 21
4.4 Canal de transmission 22
4.5 Démodulation 23
4.6 Egalisation 23
4.7 Décision sur les symboles 24
4.8 Générateurs de fréquence 24
4.9 Visualisation et mesure 24
5 Annexe : Description interne de macros Viterbi. 25
5.1 Le module Viterbi 25
5.2 Les générateurs de métriques 27
5.2.1 Les métriques euclidiennes 27
5.2.2 Les métriques de Hamming 28
1 Introduction
1.1 Généralités
Cette bibliothèque est destinée à faciliter la simulation avec MUSTIG d’une chaîne de transmission numérique de données. Ceci dans un but pédagogique ou d’étude de nouvelle structure. Toutes les fonctions de cette bibliothèque sont des macros écrites en MUSTIG, donc ouvertes et modifiables. La structure très modulaire de l’ensemble facilite la création de variantes des macros fournies.
La plupart des macros fournies ont été conçues uniquement pour la simulation. Elles nécessitent le mise en mémoire du signal complet. Elles ne sont donc pas adaptées à la simulation de signaux très longs et ni à un fonctionnement en temps réel.
1.2 Environnement
Certaines fonctions de cette bibliothèque nécessitent la version 4.5 de MUSTIG
1.3 Contenu de la livraison
Le fichier bib_com.MTG contient la bibliothèque proprement dite. Il contient toutes les macros de base.
A coté de cette bibliothèque, plusieurs fichiers présentent des exemples de simulation, à caractère didactique. Ils sont commentés dans ce document en 3.
2 Structure générale
La bibliothèque est divisée en chapitres. Chacun d’entre eux correspond à une étape de la chaîne de transmission de l’information.

2.1 Signal binaire
Contient des générateurs de signaux binaires. Un signal binaire est un signal dont les échantillons ne peuvent prendre que les valeurs "1" ou "0". En d’autres termes, c’est une suite de bits.
Bien qu’un seul bit puisse suffire à représenter ces valeurs, un signal binaire est de type "entier".
2.2 Formation des symboles
Ces macros transforment le signal binaire en une suite de symboles. Un symbole est une valeur associée à une suite de N bits.
C‘est donc encore un signal discret. Pour conserver un débit d’information constant tout le long de la chaîne, la fréquence d’échantillonnage du signal composé des symboles est N fois plus faible que celle du signal binaire.
Ces macros sont toutes décomposées en deux parties : une première qui associe N bits pour former un nombre appelé "symbole numérique". Une deuxième qui fournit une valeur correspondant à ce nombre pour le codage choisi. Cette valeur, qui représente par exemple une tension électrique, est représentée par un nombre flottant, réel ou complexe.
2.3 Modulation
Ces macros transforment la suite de symboles en un signal continu. En fait, la simulation est faite entièrement en temps discret : le continu est simulé par une augmentation importante du taux d’échantillons. A chaque symbole correspond normalement un signal continu de durée T. Il lui correspondra en fait un signal discret de M points, qui est l’échantillonné de ce signal continu.
Le signal "continu" possède donc une fréquence d’échantillonnage M fois plus grande que le signal composé des symboles.
Pour obtenir une simulation précise, on souhaitera
utiliser une grande valeur de ce facteur de sur-échantillonnage. Mais cela sera
au détriment de la vitesse de simulation. Pour pouvoir modifier cette valeur
sans ajouter systématiquement une entrée à chacune des macros, toutes ces
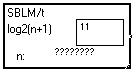
macros utilisent un report. Il est donc indispensable de définir la valeur du
report
![]() dans tous les
fichiers qui font appel à ces macros.
dans tous les
fichiers qui font appel à ces macros.
Il est important de noter que dans les équipements de télécommunication, la part du numérique (et donc du discret) est de plus en plus grande. La technique de simulation utilisée ici correspondra donc souvent à ce qui est réellement fait. Il ne manquera alors que le dernier filtrage analogique.
On trouvera dans ce chapitre des générateurs d’impulsion, des filtres, et des opérations combinées (filtres multicadences) plus rapides. Ils permettent d’effectuer une modulation en bande de base (autour de la fréquence "0"). On trouvera de plus des opérateurs pour effectuer une transposition de fréquence.
2.4 Canal de transmission
On trouvera ici la simulation des transformations effectuées sur le signal par le canal de transmission.
Ces transformations consistent en des filtrages, des retards et l’addition de bruits.
2.5 Démodulation
Ces macros transforment le signal continu en un signal à temps discret échantillonné au rythme symbole.
Elles consistent en des opérations de changement de fréquence, de filtrage et d’échantillonnage. Les opérations de filtrage et d’échantillonnage peuvent être combinées pour une meilleure efficacité.
On trouvera ici les fonctions inverses des celles du chapitre "modulation".
2.6 Egalisation
Ces macros sont destinées à compenser les déformations (qui entraînent souvent de l’interférence inter-symbole) du signal crée par le filtrage du canal.
2.7 Décision sur les symboles
En sortie des macros de démodulation, le signal est à temps discret, mais ses valeurs sont continues (en faisant abstraction de la quantification de la représentation numérique) puisque entachées de bruit.
Ces macros transforment les valeurs continues en symboles, par une opération de seuillage ou de quantification.
2.8 Générateurs de fréquence
On trouve ici des outils pour simuler l’asservissement de la fréquence d’échantillonnage (VCO)
2.9 Visualisation et mesure
On trouve ici des fonctions de visualisation spécialisées : diagramme de l’œil, tracé de constellation. Un analyseur de spectre adapté aux besoins. Des macros de comptage des erreurs de transmission.
2.10 Remarques
3 Exemples de mise en œuvre
3.1 Codage
Fichier SYMBOLES.MTG
Principe de la transmission numérique :
codage en amplitude, en quadrature, en phase ou quelconque
visualisation des constellations
addition de bruit : comptage des erreurs de transmission
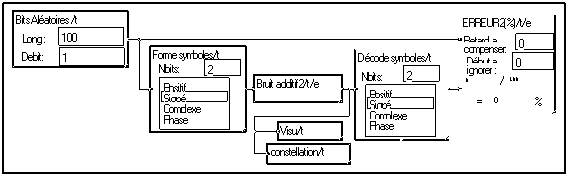
La Macro “BitsAléatoires” engendre une suite de valeurs entières de valeurs 0 ou 1. La Macro “Forme symboles” associe ces bits deux par deux et les transforme en des valeurs qui peuvent être égales à –0.75, -0.25, 0.25 ou 0.75. “Visu/t” permet d’observer le signal discret formé :
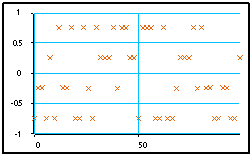
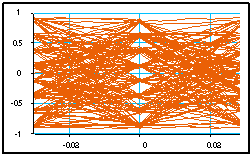
La macro “Bruit additif2” ajoute 20 réalisation de bruit (réel) à ce signal. Le signal est alors une fonction de deux variables, le temps “t” et l’indice des réalisations “e”. Sa visualisation par “Visu/t”, prévue pour un signal fonction seulement de “t”, donne une superposition des différentes réalisations de signal bruité. Chaque point du signal est remplacé par une tache :
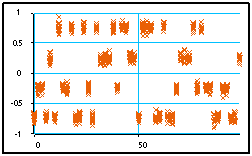
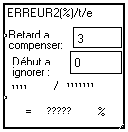
Si l’amplitude du bruit est inférieure à la moitié de l’écart entre les niveaux des symboles (ici 0.25), il est possible de reconstituer les symboles initiaux et les bits par seuillage. Cela est réalisé par la macro “Décode Symboles”. On vérifie à l’aide de la macro “ERREUR2(%)" que cela est fait sans erreur. On pourra observer que cela n’est plus le cas si on augmente la puissance de bruit ou si on resserre les niveaux en augmentant le nombre de bits par symboles.
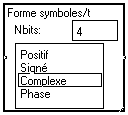
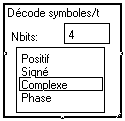
Si on choisit pour la macro “Forme symboles” un codage de type "complexe", on obtient un codage en amplitude complexe (QAM : quadrature amplitude modulation). Plutôt que de visualiser le signal temporel, on utilise alors souvent la visualisation de la "constellation". Si on choisit 4 bits par symbole et en ajoutant un bruit complexe, on obtient la figure suivante :
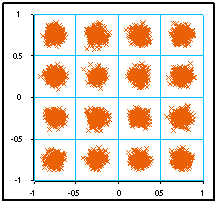
Pour effectuer des codages avec des constellations de forme différente de celles permises par “Forme symboles”, il faut utiliser “Forme symboles qque” :
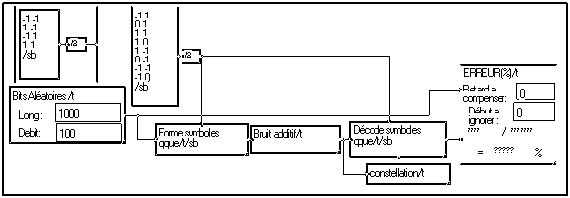
La liste des valeurs possibles des symboles est donnée sous forme d’une fonction de la variable “sb”.
La liste utilisée ci-dessus donne la constellation ci-dessous :
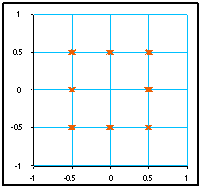
3.2 Principales méthodes de modulation (amplitude, phase)
Fichier MUSTIG MODULAT.MTG
Mise en forme par impulsions rectangulaire ou par impulsions de Nyquist.
Démodulation cohérente ou non.
Diagramme de l’œil.
3.2.1 Mise en forme par impulsions rectangulaires
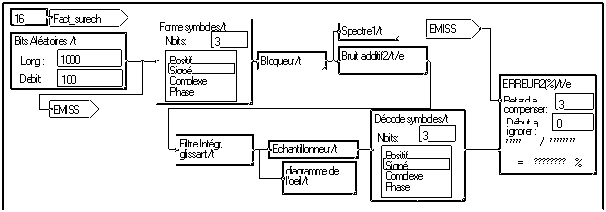
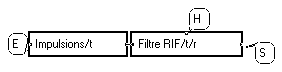
La macro "Bloqueur" associe une impulsion rectangulaire à chaque symbole ; l’amplitude de l’impulsion est la même que celle du symbole. Elle simule la fonction réalisée par les convertisseurs numériques-analogiques traditionnels.
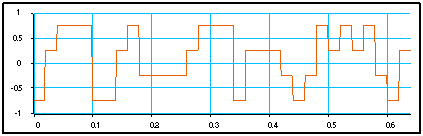
Comme il est expliqué au paragraphe 2.3, le signal formé devrait être un signal continu : il est simulé par un signal suréchantilloné. Le nombre d’échantillons par impulsion est fixé ici à 16 par le report "Fact_surech". On montre que, à la réception, il faut effectuer un filtrage adapté à l’impulsion émise avant échantillonnage. Ici, ce filtre est un intégrateur glissant sur la durée d’un symbole. Pour apprécier la qualité du signal reçu, on observe souvent le "diagramme de l'œil". Il s’agit de la forme temporelle du signal, replié par tranches de deux durées symbole. Il permet de juger de la bonne position d’instant d’échantillonnage (marqué par l ‘abscisse "0"), et de la bonne séparation des symboles à cet instant.
Notons que le filtre glissant, causal, entraine un retard d’un symbole. Il faut donc le compenser avant de comparer le signal reçu à celui émis : dans la macro “ERREUR(%)”, on fixe le retard au nombre de bits par symbole.
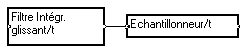
Pour des raisons d’efficacité de calcul, on a intérêt à remplacer le filtre, l'intégrateur glissant, et l’échantillonneur par une fonction combinée, la macro "Echantillonneur-moyenneur" qui ne calcule la moyenne qu’à l’instant d’échantillonnage.
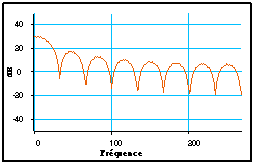
On peut observer le spectre du signal : on constate les lobes importants de ce type de modulation.
3.2.2 Mise en forme par impulsions "racine de Nyquist"
Pour diminuer l’encombrement spectral, on utilise une mise en forme par des impulsions dont l’étendue spectrale est plus faible. La durée de ces impulsions est alors nécessairement supérieure à celle d’un symbole et elles vont se chevaucher. Des formes particulières, comme l’impulsion "racine de Nyquist", évitent néanmoins l’interférence inter-symboles aux instants d’échantillonnage.
La mise en forme du signal peut se faire de façon "théorique" en remplaçant le bloqueur par un générateur d’impulsions de Dirac suivi par un filtre continu dont la réponse impulsionelle est la forme d’impulsion souhaitée.

La macro "Nyquist12" calcule les coefficients du filtre "racine de Nyquist". Pour des raisons d’efficacité, il est préférable de remplacer cette structure par un filtre multicadence qui économise les nombreux calculs sur les valeurs nulles introduites entre les impulsions de Dirac. La macro "Forme impulsion" est basée sur ce principe.
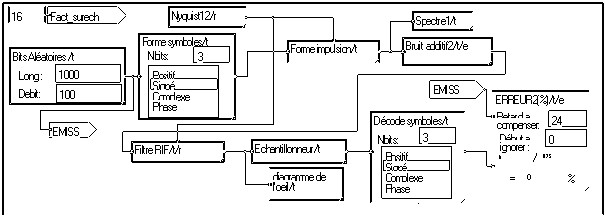
A la réception, le filtrage adapté peut être réalisé par un filtre RIF de réponse impulsionnelle racine de Nyquist. Cela simule une réalisation analogique de ce filtre et permet d’observer le digramme de l’œil.
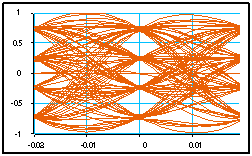
On pourra insérer un retard d’une fraction de temps symbole dans le trajet du signal "continu". On simule ainsi une erreur de synchronisation.
Pour des raisons d’efficacité de calcul, on aura intérêt à utiliser la macro "Filtre_échantillonneur" qui ne calcule que les points pris en compte par l’échantillonnage. Cela correspond à une réalisation numérique du filtrage. Il n’est plus possible alors de visualiser le diagramme de l’œil.
On peut vérifier que l’étendue spectrale du signal est bien plus faible qu’avec les impulsions rectangulaires :
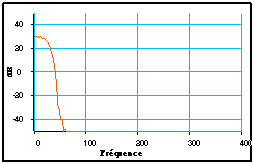
3.2.3 Modulation-Démodulation non cohérente
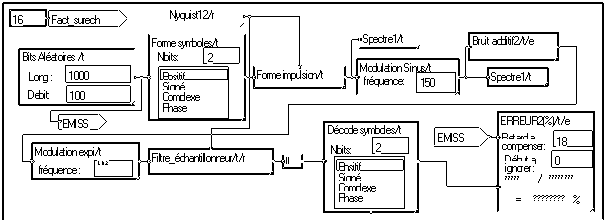
Les signaux créés par les mises en formes précédentes étaient en "bande de base" : leur spectre était centré autour de zéro. Pour translater leur spectre autour d’une fréquence plus haute, il suffit de les multiplier par une sinusoïde à cette fréquence, que l’on appelle "fréquence porteuse". C'est cette opération qui est souvent appelée "modulation". Elle est réalisée par la macro "Modulation Sinus". On peut le vérifier en observant le spectre résultant :
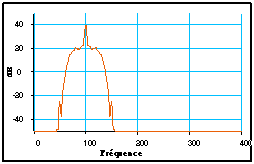
Il convient ici de veiller à avoir un facteur de sur-échantillonnage suffisant, sous peine de créer du repliement de spectre.
Pour remettre le signal en bande de base à la réception, il faut le multiplier à nouveau par une sinusoïde de fréquence égale à la fréquence centrale, puis le filtrer passe bas pour éliminer les hautes fréquences. En fait, pour être insensible à la phase, on multiplie par une exponentielle complexe (ce qui revient à multiplier séparément par une sinusoïde et par une cosinusoïde ), et on prend le module en sortie. La fonction de filtrage passe-bas est réalisée par le filtrage en racine de Nyquist L’insensibilité à la phase procure même une faible sensibilité aux erreurs de fréquence : la fréquence de démodulation peut être différente de la fréquence de modulation. Notons que l’utilisation du module du signal ne permet pas de transmettre un signe, le codage des symboles est de type "positif".
3.2.4 Modulation-Démodulation cohérente
Si on peut connaître en réception la fréquence et la phase de la porteuse d'émission, il est possible d'utiliser un codage en des symboles en amplitude et phase. On pourra utiliser les type de codage "Complexe" ou "Phase" de la macro "Forme symboles".
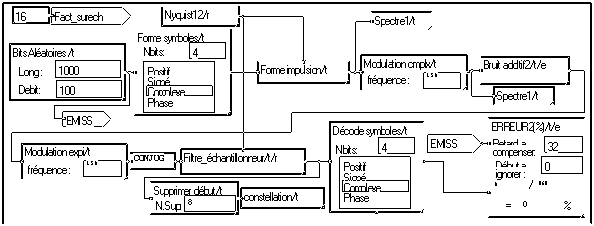
Les symboles étant complexes, la modulation est faite par la macro "Modulation complexe". Le signal résultant est toujours réel. La démodulation est encore faite par "Modulation expi", mais sans calcul du module. Notons la présence de l'opérateur "conjug", qui peut se remplacer par un signe moins devant la fréquence de démodulation.
On peut vérifier qu'une très faible erreur de fréquence (150.01 au lieu de 150) brouille complètement la constellation :
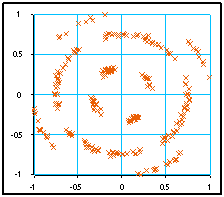
Et qu'une erreur de phase la fait tourner :
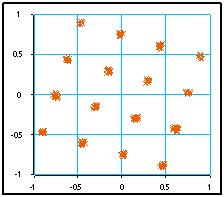
Notons que pour visualiser ces constellations, on a supprimé les premiers points qui sont faussés par les transitoires des filtres.
Ces filtres introduisent un retard qui est compensé lors de la comparaison dans la macro "ERREUR(%)".
3.3 De la modulation PSK à la modulation GMSK
Fichier MUSTIG GMSK.MTG
Modulation QPSK à 4 états.
Modulation OQPSK.
Modulation MSK vue comme variante de OQPSK.
Modulation MSK vue comme cas particulier de modulation de fréquence.
Modulation GMSK (utilisée par le GSM).
3.3.1 Modulation QPSK4
La modulation de phase en quadrature à quatre états (Quadrature Phase Shift Keying 4) est un cas particulier de ce qui a été vu en 3.2. On utilise la macro "Forme symboles cplx", plus simple que "Forme symbole", et une mise en forme par une impulsion rectangulaire.
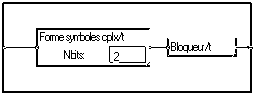
La démodulation se fait par :
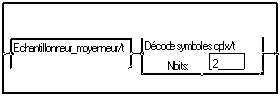
Ce signal présente l'inconvénient de présenter des transitions brutales de phase de –PI à +PI. Cela est mis en évidence par le tracé du chemin du signal dans le plan complexe, fait par la macro "Transition/t".
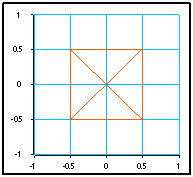
Un solution pour atténuer cela est de retarder les transitions de la partie imaginaire d'un demi temps symbole. On obtient alors la modulation OQPSK4(Offset Quadrature Phase Shift Keying 4)
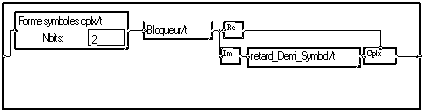
Il suffit de compenser ce retard à la réception ; (Un retard supplémentaire a été ajouté pour que le retard global soit de un symbole complet).

Le diagramme de transition montre que les discontinuités de phase sont plus faibles :

L'occupation spectrale de ce signal reste encore très grande en raison des discontinuités de phase. Pour la diminuer, on peut adoucir ces transitions. On peut obtenir la modulation MSK (Minimum Shift Keying) en remplaçant dans la modulation OQPSK l'impulsion rectangulaire formée par le bloqueur en une arche de sinusoïde.
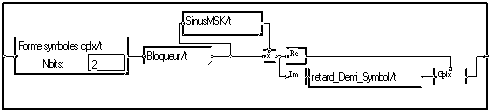
Le signal se déplace alors dans le plan complexe sur un cercle.
Le filtrage adapté en réception revient à un produit scalaire :
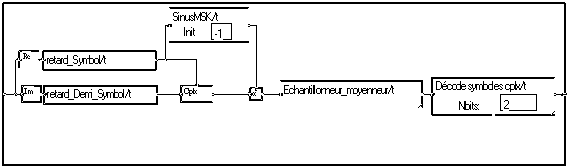
Observons le signal temporel (partie réelle superposée au signal complexe) :
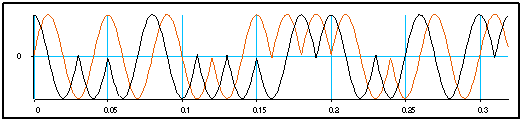
On voit que le signal ne présente pas de discontinuités. Il possède néanmoins des points de rebroussement : son spectre présentera des lobes moins prononcés que l'OQPSK, mais encore importants. On peut les réduire par la modulation GMSK.
3.3.2 Modulation GMSK
Pour introduire la modulation GMSK, il faut revenir à la modulation MSK, et la considérer comme une modulation de fréquence à phase continue ou CPFSK(Continuous Phase Frequency Keying).
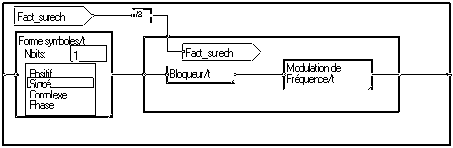
On prend les bits un par un pour commander la fréquence par la macro "Modulation de fréquence" Pour que deux bits successifs correspondent au même nombre d'échantillons après suréchantillonage par le bloqueur, le facteur de suréchantillonnage est divisé par deux.
Pour que cette modulation de fréquence donne le même résultat que la modulation de phase du paragraphe précédent, il faut dériver le train binaire. Cela est fait par la macro "dérivée logique". Pour s'affranchir de l'état initial, on compare les dérivées des signaux reçus et émis.
(En pratique, on utilisera des codes différentiels.)
La modulation GMSK s'obtient alors en lissant les changements de fréquence par un filtre de réponse impulsionelle Gaussienne. Cela est réalisé par la macro GMSK0 de l'exemple :
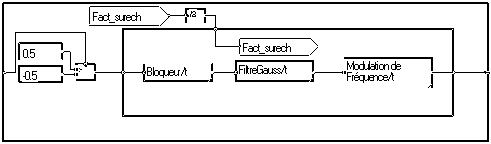
Notons le remplacement de la macro "Forme_symboles" par une forme plus simple.
En fait, on peut remplacer la juxtaposition "Bloqueur" et "FiltreGauss" par la juxtaposition "Impulsion" et "FiltreGauss". (Dans le cas général, le filtre serait différent, il est identique dans le cas du filtre de réponse impulsionelle gaussienne.) Cela est fait dans "GMSK1". Il est alors possible d'utiliser la structure plus rapide de la macro "Forme impulsion", dans la macro "Impulsion de Gauss". Cela est fait dans "GMSK" :
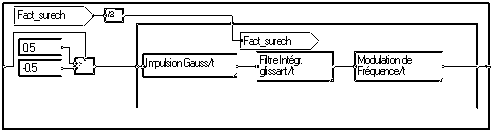
On peut voir que le spectre de ce signal est sensiblement amélioré. Mais la forme temporelle est très proche :
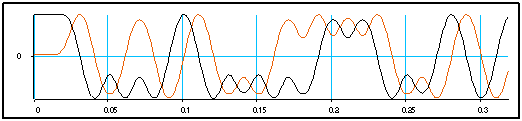
Les rebroussements ont seulement été arrondis. Il est donc possible, pour la démodulation, d'assimiler la modulation GMSK à une modulation OQPSK.
3.4 Egaliseur de lignes de transmission
3.4.1 Egaliseur transversal
Fichiers MUSTIG EGALIS.MTG,
Egaliseur par filtre adaptatif (LMS), aveugle ou avec séquence d'apprentissage.
Egaliseur de Viterbi.
Intéressons-nous à une transmission en codage QAM :
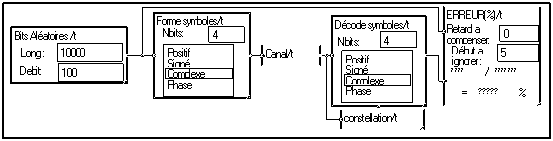
La macro "Canal" comprend un filtre et une addition de bruit. Cette simulation ne fait pas apparaître le processus de modulation proprement dit, avec la transmission d'un signal continu. Elle est entièrement discrète. Il faut considérer que la macro "Canal" représente l'ensemble du canal, y compris les modulateurs et démodulateurs.
Si on observe la constellation en sortie du canal, on voit des taches étendues qui se recouvrent partiellement : cela provoque des erreurs de transmissions.
Pour améliorer la qualité de transmission, on ajoute un égaliseur.
Une des structures les plus utilisées consiste en un filtre placé sur le chemin des données, tel que sa mise en cascade avec le filtre du canal soit équivalente à un filtre unité (A un retard près pour respecter la causalité). Il faut donc réaliser le filtre inverse de filtre du canal. Dans le cas général, ce filtre n'est pas connu et peut même évoluer au cours du temps. On utilise alors un filtre auto adaptatif.
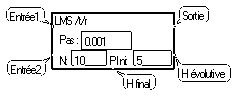
La macro "LMS" réalise un filtre adaptatif en mettant en œuvre l'algorithme du gradient :

Elle comprend un filtre à réponse impulsionelle finie de "N" coefficients entre E1 et S. L'algorithme du gradient fait converger les coefficients de ce filtre de façon à minimiser la différence entre S et E2.
Si on applique le signal reçu en E1 et le signal émis en E2, le filtre converge vers le filtre inverse du filtre du canal.
On ne dispose normalement pas du signal émis en réception, puisque c'est précisément ce que l'on cherche. Une solution est d'utiliser le signal reconstitué en sortie de l'organe de prise de décision.
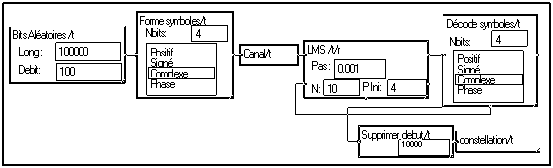
La macro "Décode symboles" fournit sur sa borne inférieure les symboles reconstitués qu'il suffit de reboucler sur la borne E2 de la macro "LMS". Il est préférable d'initialiser le filtre comme un filtre unitaire (dont la réponse du filtre est un "dirac"). La macro LMS permet de choisir le retard de ce filtre initial.
Cette technique, appelée égalisation aveugle, ne fonctionne que si le canal n'est pas trop perturbé et que le taux d'erreur est faible sans égaliseur. Sinon, il est nécessaire de faire précéder le signal utile par un signal connu à la réception : une séquence d'apprentissage. La convergence est alors possible, puisque la référence est exacte. Ensuite, on peut commuter en mode aveugle pour pouvoir suivre des non stationnarités du canal.
On utilise dans l'exemple une séquence binaire pseudo-aléatoire comme séquence d'apprentissage, qui est insérée par la macro "Concaténer". Un signal identique est reproduit en réception. La macro "Commute" applique tout d'abord ce signal à l'entrée référence de la macro LMS, puis la sortie des symboles reconstitués.
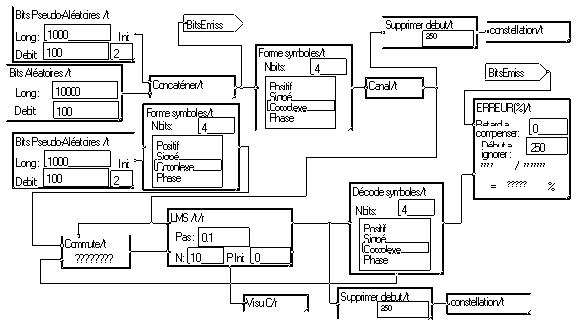
3.4.2 Egaliseur de Viterbi
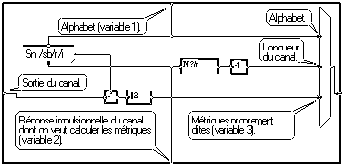
Le graphe ci-dessous montre un cas des plus simples de mise en œuvre de la macro "Egalis.Viterbi".
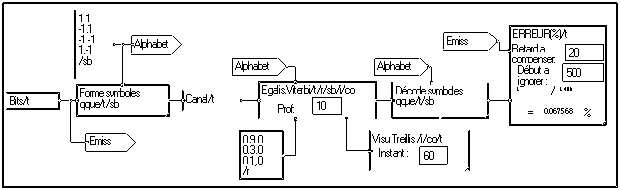
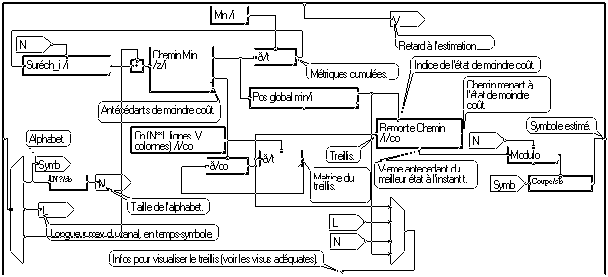
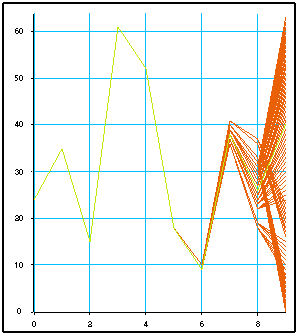
Le train de bits est transformé en symboles par la macro "Forme Symbole qque", qui permettrait un codage avec alphabet quelconque. En fait le codage est ici simplement QPSK à 4 états. La macro canal comporte un bruit additif et un filtre à réponse impulsionnelle finie de coefficients 0.9, 0.3, 0.1. La macro Viterbi fournit en sortie les symboles reconstitués. Ils sont transformés en bits par "Décode symboles qque". On suppose ici connaître le filtre du canal : sa réponse impulsionnelle est communiquée à la macro Viterbi. La visualisation "Visu Treillis" permet d'observer le fonctionnement de l'algorithme de Viterbi. On voit la convergence vers un chemin unique.
Si on ne connaît pas la réponse impulsionnelle du canal, il faut l'identifier, en faisant précéder le signal par une séquence d'apprentissage.
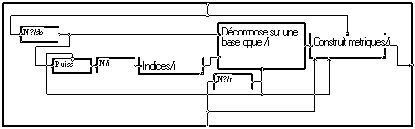
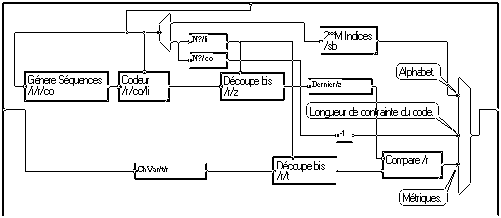
L'identification peut se faire par la macro " LMS" comme ci-dessous.
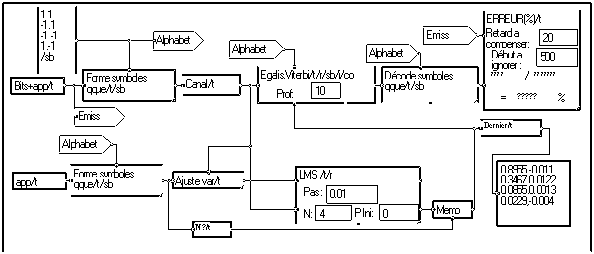
La macro "Bits+app" génère le signal binaire précédé de la séquence d'apprentissage. La macro "app" génère une copie de cette séquence. Notons que le branchement de la macro "LMS" est différent de son branchement en égaliseur. Dans le cas de l'égaliseur, on cherche à identifier un filtre inverse, alors qu'ici, on cherche à identifier le filtre lui-même. La macro "Ajuste var" prolonge cette séquence à la longueur du signal. La macro "Memo" mémorise la réponse identifiée par le LMS à la fin de la séquence d'apprentissage.
3.5 Modulation multifréquence (DMT ou OFDM)
Exemple MUSTIG OFDM.MTG
Etalement de spectre par codage (CDMA)
Modulation multi-fréquences
Cas particulier multifréquence (calculée par DFT)
DMT réel
DMT complexe
Note : Compte tenu des nombreuses variantes possibles, il n'y a pas de macro complète dans la bibliothèque concernant ces modulations, mais seulement des macros très élémentaires. Il faudra partir des exemples ci-dessous pour construire la chaîne de traitement désirée.
3.5.1 Etalement de spectre (CDMA)
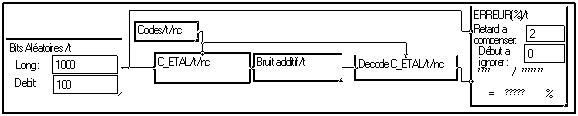
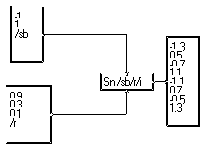
La macro "C_ETAL" ressemble à la macro "Forme Symbole qque". Elle commence également par associer plusieurs bits successifs pour former un nombre ("symbole numérique"), mais ensuite, au lieu de choisir une valeur dans un alphabet, elle choisit un signal composé de plusieurs valeurs successives:
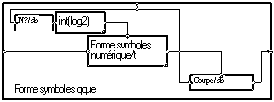
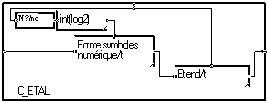
L'alphabet et alors une liste de signaux. Elle est fournie par la macro "Codes/t/nc". C'est donc un ensemble de signal fonction de la variable 't' et indicé par la variable 'nc'. Ici, nous avons choisi des codes binaires pseudo-orthogonaux. Nous obtenons dons un codage de type "CDMA". Nous pourrions mettre un ensemble de sinusoïdes. Nous obtiendrions alors une simple modulation de fréquence ( à phase discontinue).
Pour faire le décodage, on pourrait construire l'ensemble des filtres adaptés à chacun des signaux de l'alphabet, d'échantillonner leur sortie à la fin d'un symbole, et de choisir la sortie la plus forte. C'est ce qui est fait dans la macro "Décode C_ETAL(principe)" de l'exemple. La macro " Décode C_ETAL" utilise un simple produit scalaire, plus rapide.
3.5.2 Modulation multifréquence
Dans l'exemple ci-dessus, on transmet l'un ou l'autre des signaux de l'alphabet. On peut transmettre une combinaison linéaire de ceux-ci.
La macro "C_PROJ" de l'exemple réalise cela :
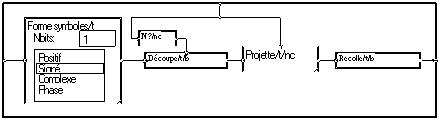
.
La macro "Forme symboles" génère une suite de symboles scalaires. Ces symboles sont ensuite groupés en paquets par "Découpe". La taille de ces paquets est égale au nombre de signaux de l'alphabet. On pondère chacun des signaux de l'alphabet par le scalaire correspondant. Cela revient à réaliser une projection sur une base, qui pourrait se formaliser par un produit de matrice. Cela est fait par la macro "Projette" qui associe à chaque paquet un nouveau paquet de taille égale à la taille des signaux de l'alphabet. On appellera ces paquets des "trames". "Recolle" forme un signal en raboutant ces trames.
La macro Décode C_PROJ effectue le décodage.
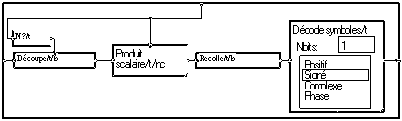
"Découpe" reforme les paquets de taille égale à la taille des signaux de l'alphabet. La macro "Produit scalaire" effectue l'opération inverse de la projection, en supposant les signaux de l'alphabet orthogonaux entre eux.
L'exemple "MCODE(projection)" met cela en œuvre avec un alphabet de code binaire. Dans les exemples "DMT", on utilise les mêmes macros, avec une base de signaux sinusoïdaux. On peut montrer que si on respecte une condition particulière d'espacement des fréquences de l'alphabet de signaux (qui est précisément la condition d'orthogonalité), la projection sur la base est équivalente à une transformée de Fourier discrète (DFT). En utilisant la transformée de Fourier rapide (qui est mise en œuvre dans le module "TF" de MUSTIG), on augmente considérablement la vitesse de simulation. Cela est réalisé dans la macro "OFDMcplx" :

On a remplacé la macro "Projette" par les macros "Met en fréquence" et "DFTI".
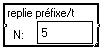
"Met en fréquence" comprend principalement un changement de variable : les paquets formés par "Découpe" sont alors considérés comme des valeurs en fréquence. Ces valeurs sont complétées à la taille de la TFD par des valeurs nulles. Cette taille, que nous appellerons taille de trame brute, est paramétrable sur le devant de "Met en fréquence". La macro "DFTI" réalise la DTF à l'aide du module élémentaire "TFI", complétée par une normalisation. Une macro "Préfixe…" a été ajoutée pour effectuer diverses manipulations sur les trames. On peut prolonger celle-ci par des valeurs nulles (intervalle de garde). On peut ajouter un préfixe cyclique, et on peut effectuer une pondération. Le nombre d'échantillons ajoutés par ces opérations est compté et affiché. Il devra être identique à celui donné à la macro "Met en fréquence". (Celle-ci utilise ce paramètre pour affecter le pas de la variable fréquence, ce qui permet de visualiser le signal fréquentiel avec des échelles correctes.) On affiche la taille des trames résultantes. Cette valeur devra être reportée dans la macro de décodage pour découper à nouveau le signal en trames de même longueurs.
Le décodage est effectue par la macro "Décode OFDMcplx" avec les opérations inverses :
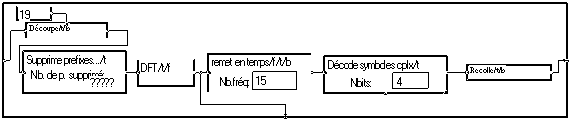
La taille du découpage en trame doit être fournie en paramètre. On utilisera la valeur retournée par la macro "OFDMcplx". Dans la macro "remet en temps", on affiche le nombre de symboles utiles en sortie de DTF. C'est la taille du découpage à l'entrée de OFDMcplx"
La mise en œuvre la plus simple de ces macros est la suivante :
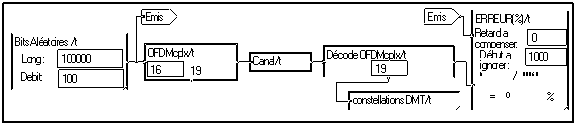
Si le nombre de fréquences utilisées (c'est à dire la taille de la TFD) n'est pas trop grand, on peut observer simultanément les constellations de toutes les fréquences. On dispose pour cela de la macro "constellations DMT".
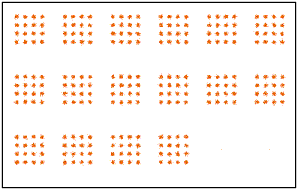
Si on fait passer le signal dans un canal qui modifie l'amplitude et la phase du signal, on peut observer les modifications :

Pour décoder correctement un tel signal, il est nécessaire d'effectuer une égalisation. Celle-ci peut avantageusement s'effectuer dans le domaine des fréquences. Elle consiste alors à appliquer un gain complexe sur chaque composante.
Dans la "macro "Décode OFDMcplx+egal" a été ajouté un tel égaliseur :
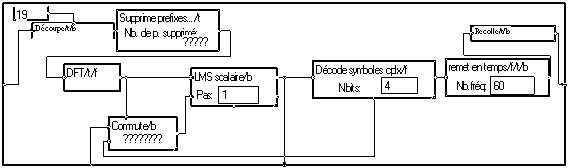
La macro "Commute" applique tout d'abord la séquence d'apprentissage comme signal de référence du "LMS". Ensuite, ce sont les symboles estimés par "Décode symbole" qui en tiennent lieu (fonctionnement en "aveugle"). Notons que la macro "Décode symbole" a été déplacée devant la macro "remet en temps". Cela nécessite d'afficher en paramètre de celle-ci le nombre de symboles utiles en fréquence multiplié par le nombre de bits par symboles.
Cette égalisation est mise en œuvre de la façon suivante :
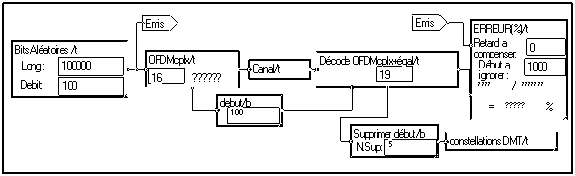
On utilise comme séquence d'apprentissage le début du signal. Ce signal, dans le domaine des fréquences, est pris sur une borne de la macro OFDM. Pour rendre la simulation plus réaliste, il conviendrait de dupliquer ce codage du coté de la réception. Pour visualiser les constellations, on supprime les premières trames qui correspondent à la phase d'apprentissage.
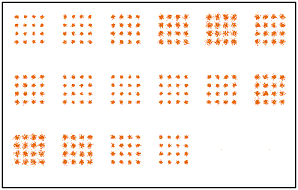
Les macro précédentes "OFDMcplx" et "DécodeOFDcplx" simulent la transmission d'un signal de type complexe, constitué de deux composantes, qui servira en pratique à moduler une porteuse.
Les macros "OFDMreel" et "DécodeOFDMréel" du sous exemple DMT(OFDM) réel simulent la transmission d'un signal réel. Les symboles fréquentiels sont considérés comme une fonction d'une variable de type "demi", dont la transformée Fourier inverse est un signal réel.
3.6 Synchronisation
Les fonctions de récupération de porteuse et de synchronisation symboles ne sont pas intégrées à la version 1 de cette bibliothèque. On trouvera seulement quelques exemples non commentés.
4 Descriptions détaillées
On trouvera dans ce chapitre les descriptions des macros de la bibliothèque. Ces descriptions sont disponibles sous MUSTIG par la commande "Lire les informations" (Ctrl H)