

BIBLIOTHEQUE
Ondelettes
Version 1.0
Bibliothèque ONDELETTES pour MUSTIG
Table des Matières
Installation de la bibliothèque Ondelettes pour MUSTIG
INTRODUCTION
I. L'ANALYSE CONTINUE PAR ONDELETTES
1.1. Rappels sur l'analyse de Fourier
1.1.1. La Transformée de Fourier
1.1.2. La Transformée de Fourier à Court Terme (TFCT)
1.2. Transformée Continue en Ondelettes (T.C.O.)
1.2.1. Notions d'échelle et de position
1.2.2. La Transformée Continue en Ondelettes
1.2.3. Mise en œuvre sous MUSTIG
1.2.4. Ondelettes et résolution temps-échelle
1.2.5. Représentation "en résolution vraie" de la R.T.E.
1.2.6. Comment choisir l'ondelette de référence ?
1.2.7. Choix des valeurs de a et b
1.2.8. Conclusion
1.3. Transformée Inverse Continue en Ondelettes (T.I.C.O.)
1.3.1. Pourquoi une transformée inverse ?
1.3.2. Expression de la transformée inverse
1.3.3. Module MUSTIG
1.3.4. Exemple
II. La Transformée en Ondelettes Discrète
2.1. Notion de détails et d'approximation
2.2. Analyse multirésolution
2.3. Transformée inverse
2.4. Le problème des effets de bord
2.5. Transformée rapide ou Fast Wavelet Transform
2.5.1. Module MUSTIG
2.5.2. Disposition des coefficients d'ondelettes
2.5.3. Séparation de l'approximation et des différents niveaux de détails
2.5.5. Mise en œuvre de la transformée inverse
2.6. A quoi ressemblent les ondelettes et les fonctions d'échelle ?
2.7. Analyse multirésolution à 2 dimensions
2.7.1. Principe
2.7.2. Module MUSTIG
2.7.3. Interprétation des résultats
2.7.4. Transformée 2D inverse
2.7.5. Allure des ondelettes 2D
2.8. Conclusion
III. Algorithmes de seuillage des coefficients
3.1. Principe général
3.2. Seuillage brut ou "hard thresholding"
3.3. Rétrécissement ou "soft thresholding" ou "shrinkage"
3.4. Détermination du seuil à utiliser
3.4.1. Seuil absolu
3.4.2. Seuil relatif
3.4.4. Seuil quantitatif absolu
3.4.4. Seuil quantitatif relatif
3.4.5. Seuil universel ou "seuil de Donoho"
3.5. Modules MUSTIG de seuillage des coefficients
3.6. Comment séparer et seuiller les coefficients ?
3.7.1. Cas monodimensionnel
3.7.2. Cas bidimensionnel
3.7. Comment évaluer l'efficacité du seuillage ?
3.8. Comment traiter séparément les détails horizontaux, verticaux et diagonaux d'une transformée 2D ?
3.9. Exemple à une dimension
3.10. Exemple à deux dimensions
IV. TRANSFORMEE EN PAQUETS D'ONDELETTES
4.1. Mise en oeuvre
4.2. Fonctions de coût entropiques
4.3. Sélection de la combinaison de noeuds optimale
4.3.1. Méthode des bases d'ondelettes
4.3.2. Méthode du meilleur niveau (Best Level)
4.3.3. Méthode de la meilleure base (Best Basis)
4.4. Mise en œuvre sous MUSTIG
4.4.1. Transformée en Paquets d'Ondelettes Directe
4.4.2. Sélection des noeuds
4.4.3. Transformée en Paquets d'Ondelettes Inverse
4.4.4. Débruitage par décomposition en Paquets d'Ondelettes
ANNEXE 1 : Liste des modules de la bibliothèque ONDELETTES pour MUSTIG
ANNEXE 2 : Liste des exemples fournis
INDEX de la bibliothèque Ondelettes pour MUSTIG
Remarques / Suggestions
Installation de la bibliothèque Ondelettes pour MUSTIG
Versions compatibles
Pour utiliser la bibliothèque Ondelettes, vous devez posséder la version 4.5 de MUSTIG. Dans le cas contraire, vous ne pourrez pas utiliser la totalité des fonctionnalités à votre disposition..
Installation de la bibliothèque
Insérez la disquette fournie dans le lecteur et lancez le programme A:\INSTALL.EXE
L'installation de la bibliothèque et des DLL associées est automatique dans le répertoire choisi.
Externes
Cette bibliothèque utilise trois programmes externes écrits en C. Assurez-vous lors de l'utilisation que ces programmes sont accessibles soit dans votre répertoire de travail, soit dans l'un des répertoires définis en Options / Chemins dans MUSTIG.
Les deux principaux domaines de représentation utilisés en Traitement du Signal sont le Temps (exprimé en unité physique ou en nombre d'échantillons) et la Fréquence (en Hertz ou en fraction de la fréquence d'échantillonnage du signal). L'outil désormais classique permettant de passer d'un domaine à l'autre est la Transformée de Fourier (TF).
La TF permet d'estimer les fréquences présentes dans un signal, mais pas de localiser l'endroit où ces fréquences apparaissent ou disparaissent, car elle agit sur la totalité du signal. Pour disposer d'une information de type temps-fréquence, c'est-à-dire à la fois en temps et en fréquence, il faut calculer la TF d'une fenêtre de petite taille que l'on fait "glisser" d'un bout à l'autre du signal. On obtient alors une représentation temps-fréquence de type spectrogramme.
L'inconvénient de cette procédure, outre sa faible résolution conjointe temps / fréquence, est que la taille de la fenêtre est constante. Il serait plus pertinent d'adapter la taille de la fenêtre d'analyse aux caractéristiques locales du signal : petite fenêtre lorsque le signal varie rapidement (hautes fréquences) et plus grandes fenêtre lorsque ses variations sont lentes (basses fréquences).
L'analyse en Ondelettes vise à apporter une solution à ce problème en décomposant le signal sur une base de signaux élémentaires (les fameuses Ondelettes) obtenus par dilatation et décalage d'une ondelette de base. En modifiant ainsi par dilatations ou contractions successives la taille de l'ondelette analysante, il est possible de détecter des détails localisés plus facilement qu'avec la TF.
Cette approche par déformation et déplacement d'une ondelette de base, appelée Transformée Continue, est la plus intuitive et permet de bien saisir les concepts sous-jacents à l'analyse par Ondelettes. Elle est présentée de façon détaillée au chapitre I.
Cependant, l'approche la plus utilisée consiste à filtrer le signal en cascade par un banc de filtres passe-bas et passe-haut complémentaires. Cette méthode, appelée Transformée Discrète ou encore Analyse Multirésolution, produit par filtrages et décimations successifs une série de signaux correspondant à une résolution de plus en plus faible, i.e. à des fréquences de plus en plus basses. Cette approche est décrite au chapitre II.
Le chapitre III est consacré aux méthodes de seuillage qui permettent, en annulant les coefficients d'ondelettes les moins significatifs, de débruiter ou de comprimer des signaux ou des images.
Enfin, au chapitre IV, une extension de l'analyse multirésolution est présentée. L'analyse par Paquets d'Ondelettes permet d'atteindre des performances de débruitage ou de compression encore supérieures.
Tout au long de ce manuel, les passages didactiques alterneront avec les descriptions techniques des modules MUSTIG de la bibliothèque Ondelettes. Un grand nombre d'outils de base vous sont proposés, ainsi que des applications intégrées prêtes à l'emploi (débruitage, analyse temps-échelle). Bien entendu, les modules de cette bibliothèque sont déverrouillables et modifiables, vous pouvez donc facilement réaliser vos propres applications à partir des modules proposés.
En fin de volume, un tableau reprend l'ensemble des modules de cette bibliothèque. Utilisez-le pour une référence rapide.
Dans un but pédagogique, un certain nombre d'exemples et d'applications vous sont également proposés sous la forme de petits programmes MUSTIG.
I. L'ANALYSE CONTINUE PAR ONDELETTES
1.1. Rappels sur l'analyse de Fourier
1.1.1. La Transformée de Fourier
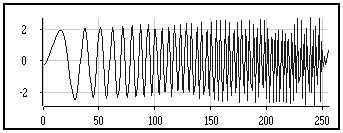
La transformée de Fourier (TF) est l'un des outils les plus utilisés par la communauté du Traitement du Signal. Elle permet, en décomposant le signal selon un ensemble de sinusoïdes, de passer du domaine temps au domaine fréquence. Dans l'exemple ci-dessous, le signal est une sinusoïde de fréquence 0.05 Hz, centrée dans une fenêtre de bruit blanc.
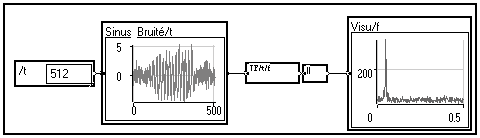
Le module de la Transformée de Fourier du signal présente un pic dont la position indique la fréquence de la sinusoïde. En revanche, l'information temporelle est perdue : la transformée de Fourier ne permet pas de connaître les dates d'émergence et de disparition de la sinusoïde dans le bruit. En effet, les sinusoïdes ne sont pas localisées dans le temps, elles ne peuvent donc pas prendre en compte le caractère non stationnaire du signal.
1.1.2. La Transformée de Fourier à Court Terme (TFCT)
Pour obtenir de l'information à la fois en temps ET en fréquence, une solution est de partager le signal en "tranches" de longueur donnée, d'effectuer une TF de chaque tranche de signal, puis de juxtaposer les résultats sous la forme d'une Représentation Temps-Fréquence (RTF). Sur l'axe horizontal on porte le numéro de la fenêtre (i.e. le "temps") et sur l'axe vertical la fréquence. Le module de la TF est alors une troisième dimension que l'on représente à l'aide d'un code couleur, de courbes de niveau, ou bien d'un graphique en trois dimensions.
Reprenons notre exemple avec une fenêtre glissante de 64 échantillons :
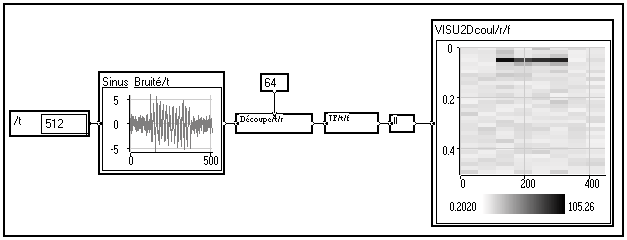
Cette fois, la fréquence et la position temporelle de la sinusoïde sont bien visibles, l'information est plus complète.
Ce type de RTF, obtenue en calculant la TF d'une fenêtre glissante, est appelée spectrogramme. Il s'agit d'un des outils de base de l'analyse de signaux non stationnaires. Le choix de la longueur de la fenêtre d'analyse est guidé par la connaissance a priori sur le signal. En effet, on suppose que le signal est stationnaire (i.e. son spectre ne change pas) sur chaque fenêtre.
La précision avec laquelle sont déterminées les fréquences et les positions est guidée par le principe d'incertitude de Heisenberg. Plus la fenêtre est longue, plus la précision en fréquence est élevée, mais plus la précision temporelle est faible. Il s'agit donc de trouver un compromis entre les résolutions temporelle et fréquentielle.
En analyse TFCT, la taille de la fenêtre est toujours la même, elle ne dépend pas de la fréquence. Autrement dit, la précision en temps et en fréquence est identique pour les hautes et les basses fréquences. Les ondelettes permettent de pallier à cet inconvénient en adaptant la précision en fonction de la fréquence.
1.2. Transformée Continue en Ondelettes (T.C.O.)
1.2.1. Notions d'échelle et de position
Plutôt qu'un ensemble de sinusoïdes de durée théorique infinie, l'analyse par ondelettes utilise une collection de fonctions localisées en temps. C'est-à-dire que la fonction sur laquelle on va projeter le signal est nulle en dehors d'un certain intervalle. Elle possède de plus les propriétés suivantes :
· son intégrale est nulle (centrage)
· l'intégrale de son module carré vaut 1 (normalisation)
La notion de fréquence est remplacée par la notion d'échelle : pour tenir compte des hautes et des basses fréquences, on va tout simplement contracter ou dilater l'ondelette de référence y (t). L'exemple ci-dessous montre l'une des ondelettes de la bibliothèque MUSTIG (l'ondelette Mexican Hat), avec différents facteurs de dilatation :

La position de l'ondelette à une échelle donnée peut facilement être modifiée en décalant simplement l'ondelette :
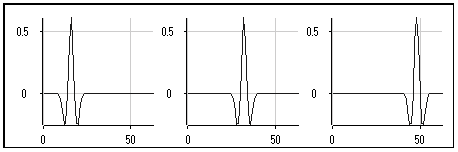
Nous avons donc deux paramètres en jeu :
· le facteur d'échelle (ou de dilatation) a, relié à la notion de fréquence
· le décalage b, relié à la notion de position temporelle.
Nous pouvons désigner par y a,b(t) l'ondelette obtenue par dilatation d'un facteur a>0 et décalage d'une position b de l'ondelette de référence y (t) :
![]()
Plus a est grand, plus l'ondelette est dilatée. Par conséquent les grandes valeurs de a seront logiquement associées aux basses fréquences, les plus petites aux hautes fréquences.
1.2.2. La Transformée Continue en Ondelettes
Nous sommes en terrain familier puisque nous avons retrouvé les notions de fréquence et de position qui apparaissent dans la TFCT. Néanmoins nous n'avons pas encore défini la Transformée Continue en Ondelettes. Il s'agit de trouver une grandeur Ca,b qui quantifie la ressemblance du signal à analyser x(t) avec l'ondelette y a,b(t).
Cette grandeur, c'est tout simplement le produit scalaire ![]() , opérateur de projection classique :
, opérateur de projection classique :
![]()
Bien que n'ayant aucune signification physique, le coefficient Ca,b sera d'autant plus élevé en valeur absolue que la similitude entre x(t) et y a,b(t) sera importante.
Le calcul de la transformée en ondelettes d'un signal se ramène donc au calcul d'une série de produits scalaires. Les étapes à suivre sont les suivantes :
1.2.3. Mise en œuvre sous MUSTIG
Les capacités multidimensionnelles de MUSTIG sont tout à fait adaptées à l'analyse continue en ondelettes. Reprenons l'exemple de l'ondelette Mexican Hat : la macro

permet de générer cette ondelette pour un facteur de dilatation a et un décalage b donné. Il suffit donc, pour générer une famille d'ondelettes y a,b(t), d'entrer directement sur les bornes supérieures un vecteur de facteurs de dilatation et un vecteur de décalages.
Vous pouvez soit entrer une liste de valeurs discrètes en utilisant le module
Val, soit entrer un vecteur de valeurs continues générées par exemple grâce au module Indices (cf. documentation MUSTIG).Exemple
Dans l'exemple ci-dessous, on utilise la première méthode pour entrer trois valeurs du facteur de dilatation selon la variable a (1, 5 et 20). La deuxième méthode est utilisée pour entrer dix valeurs du décalage selon la variable b (0 à 225 par pas de 25). La macro
VisuNv/t/a permet de visualiser toute la collection d'ondelettes ainsi produite, classée par valeurs du facteur d'échelle. La macro PS calcule le produit scalaire entre chaque ondelette et le signal d'entrée (ici une modulation linéaire de fréquence croissante) en tenant compte du pas de la variable.On obtient en sortie une matrice de coefficients d'ondelettes en fonction des variables a (facteur d'échelle, axe vertical) et b (décalage, axe horizontal), dont on visualise la valeur absolue grâce au module
Visu2Dcoul. Cette représentation est appelée Représentation Temps-Echelle (RTE) du signal par rapport à l'ondelette de référence. La relation exacte échelle / fréquence dépend de l'ondelette choisie, mais on a toujours :
· Facteur d'échelle élevé Û basses fréquences Û tendances à long terme
· Facteur d'échelle faible Û hautes fréquences Û détails, variations rapides
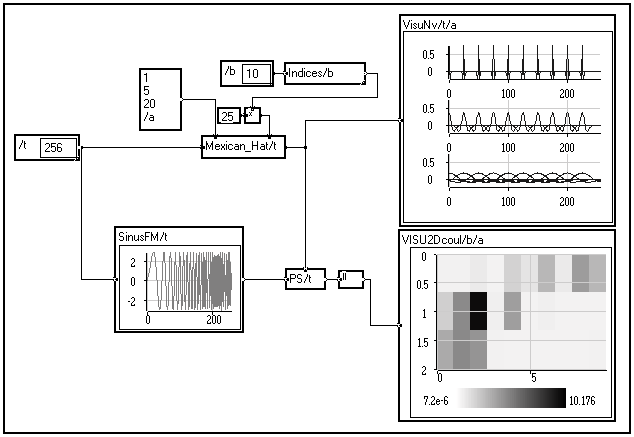
Interprétation
L'interprétation de la matrice de coefficients d'ondelettes est ici très simple. En début de signal (faible valeurs du décalage b), les coefficients les plus élevés en valeur absolue correspondent aux valeurs maximales du facteur de dilatation, c'est-à-dire aux basses fréquences. Lorsqu'on progresse vers la fin de signal, les forts coefficients "migrent" vers les faibles valeurs du facteur de dilatation, donc vers les hautes fréquences. Ceci est bien cohérent avec les caractéristiques du signal : la fréquence croît avec le temps.
1.2.4. Ondelettes et résolution temps-échelle
Plus le facteur de dilatation a est élevé, plus l'ondelette est étendue selon l'axe du temps, et plus elle est concentrée selon l'axe des fréquences. Par conséquent, la précision en temps et en fréquence est variable en fonction du facteur d'échelle a :
|
Facteur d'échelle |
fréquence |
précision en temps |
précision en fréquence |
|
faible |
haute |
élevée |
faible |
|
élevé |
basse |
faible |
élevée |
Le pavage du plan temps-échelle n'est donc pas régulier comme celui du plan temps-fréquence :
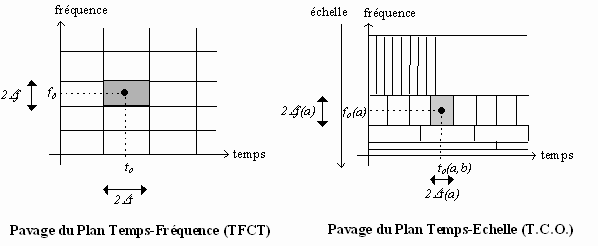
La résolution temporelle est donc plus importante pour les hautes fréquences que pour les basses fréquences. Inversement, la résolution fréquentielle est plus importante pour les basses fréquences que pour les hautes fréquences.
La position sur l'axe horizontal d'un pavé élémentaire de la R.T.E. dépend bien sûr du décalage b, mais aussi du facteur d'échelle a. Sa position sur l'axe vertical dépend elle aussi du facteur d'échelle a. De même, les dimensions du pavé (résolution de l'ondelette y a,b ) dépendent du facteur d'échelle a.
1.2.5. Représentation "en résolution vraie" de la R.T.E.
Pour interpréter l'information produite par la Transformée Continue en Ondelettes, il peut être intéressant de convertir les échelles en fréquence, car la fréquence est une notion physique plus facilement interprétable que la notion d'échelle, et indépendante de l'ondelette choisie.
Pour ce faire, il est nécessaire de visualiser les coefficients d'ondelettes en respectant le pavage du plan temps-échelle. Il faut donc calculer, pour chaque valeur du coefficient de dilatation a, les largeurs du pavé selon l'axe du temps (D t) et selon l'axe des fréquences (D f) ainsi que les positions selon les axes.
En fait, il suffit de faire le calcul pour une seule des ondelettes y a,b, car les résolutions des autres ondelettes peuvent en être déduites. La macro qui effectue ce calcul est :
![]()
Partant d'une collection d'ondelettes y a,b présentée sur sa borne gauche, la macro sélectionne celle dont l'intégrale du module carré est la plus proche de 1. Sur cette "meilleure" ondelette y a',b', on estime to, D t, D f, et fo à l'aide des formules suivantes :
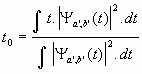
![]()
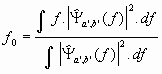
![]()
où ![]() est la transformée de Fourier de y
a',b'(t).
est la transformée de Fourier de y
a',b'(t).
Ces valeurs sont ensuite corrigées en fonction du facteur d'échelle a' pour donner la position spectrale et les résolutions temporelle et spectrale de l'ondelette de référence (i.e. celle correspondant à a = 1). Ces trois valeurs sont présentées sur la sortie droite du module sous la forme d'un faisceau.
La macro de visualisation
Visu_PTE à été construite à partir de la macro Visu2Dcoul de la bibliothèque standard pour reconstituer le pavage variable du plan temps-échelle :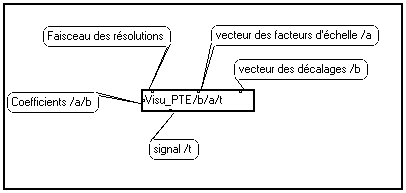
Exemple
Visualisation en résolution vraie d'une T.C.O. d'une modulation linéaire de fréquence croissante entre 0.05 et 0.4 Hz :
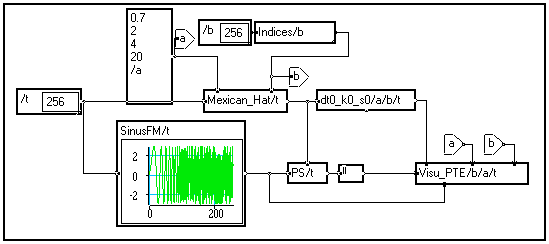
Résultat de la macro
Visu_PTE :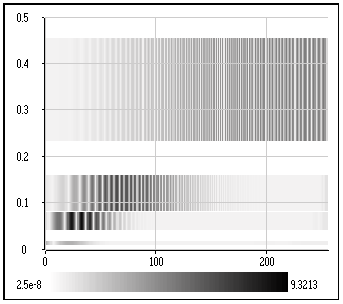
Interprétation
Une représentation en résolution vraie est parfois moins esthétique qu'une simple représentation temps-échelle, mais elle présente beaucoup d'avantages. En effet, elle permet de se rendre compte immédiatement si les vecteurs de facteurs d'échelle et de décalage sont bien adaptés au signal.
Dans l'exemple ci-dessus, les positions spectrales et temporelles sont cohérentes avec les caractéristiques du signal (modulation croissante entre 0.05 et 0.4 Hz). Cependant, il est clair que certaines zones du plan temps-fréquence ne sont pas couvertes (bandes blanches horizontales). Le vecteur de facteurs d'échelle choisi n'est donc pas apte à bien représenter toutes les caractéristiques du signal. On pourra donc modifier ce vecteur jusqu'à trouver un jeu de valeurs satisfaisantes.
De plus, la représentation en résolution vraie permet de guider le choix de l'ondelette de référence : certaines ondelettes sont plus concentrées en temps ou en fréquence que d'autres. On peut donc choisir son ondelette de référence en fonction de la couverture réelle du plan qu'elle produit.
1.2.6. Comment choisir l'ondelette de référence ?
Une infinité d'ondelettes est à votre disposition ! Cette bibliothèque vous propose les ondelettes les plus utilisées, mais rien ne vous empêche de rajouter votre propre ondelette. Le choix de l'ondelette peut être délicat, mais il est très important car il conditionne la qualité des résultats obtenus.
Votre choix peut être guidé par :
· un bon compromis de résolution temps / fréquence,
· ses propriétés mathématiques : moments nuls, régularité, ...
· une forme proche d'un motif que l'on veut mettre en évidence dans le signal sans
en connaître exactement l'échelle.
1.2.7. Choix des valeurs de a et b
Si l'on souhaite simplement analyser un signal non stationnaire, on peut produire sa Représentation Temps-Echelle en utilisant des vecteurs de facteurs d'échelle et de décalages très longs et variant selon un pas faible. La représentation obtenue contient alors beaucoup d'information redondante. Mis à part le problème du temps de calcul, cette redondance facilite souvent l'interprétation.
La plupart du temps, toutefois, la décomposition selon une collection d'ondelettes n'est que la première étape d'un processus plus complexe de compression de données ou de débruitage, qui implique une phase de décomposition, une phase de traitement des coefficients (seuillage par exemple), puis enfin une phase de reconstruction du signal.
La question est donc : quel jeu de facteurs d'échelle et de décalages doit-on choisir pour obtenir une décomposition en coefficients d'ondelettes complète (pour permettre une bonne reconstruction), mais sans redondance (pour économiser du temps de calcul) ?
On choisit pour cela de fixer un pas ao de variation de l'échelle et un pas bo de variation du décalage, et de prendre :
· a = aom
· b = nboa = nboaom
où m et n sont des entiers relatifs variant entre des bornes fixées par l'utilisateur. On notera que le décalage dépend du facteur d'échelle, ce qui est cohérent avec le pavage irrégulier du plan (cf. §1.2.4). L'ensemble des fonctions y ab ou y mn ainsi créé, sous certaines conditions, permet la reconstruction du signal de départ.
En pratique, pour réduire la redondance, on choisit ao et bo de telle sorte que les fonctions y mn forment une base orthonormée. En général on prend :
ao = 2
bo = 1
Ainsi, le facteur d'échelle varie de façon dyadique, c'est-à-dire en puissances de 2, ce qui permet la reconstruction du signal.
Une macro de la bibliothèque Ondelettes permet de générer facilement une collection de valeurs am et bn,m à partir des racines ao et bo, et de deux rampes d'entiers relatifs définissant les variations de m et n :
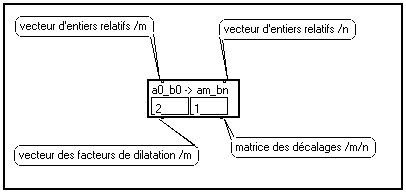
Choix des bornes pour m et n
Les bornes de variation des entiers relatifs m (exposant facteur d'échelle) et n (niveau de décalage) sont fixés en fonction des caractéristiques de l'ondelette.
Si un facteur d'échelle est trop grand, l'ondelette correspondante est mal adaptée car elle "déborde" du support du signal. Inversement, si l'échelle est trop petite, elle sera sous-échantillonnée, donc également mal adaptée au signal.
De même, si le décalage est trop grand, l'ondelette associée à cette valeur est mal centrée, son intégrale sur le support du signal n'est pas nulle, et le coefficient calculé n'a pas de signification. Inversement, si le décalage maximal est trop petit, les hautes fréquences en fin de signal ne seront pas estimées.
Là encore, la représentation "en résolution vraie" est d'une aide précieuse car elle aide à détecter les valeurs mal adaptées de m et n.
Exemple
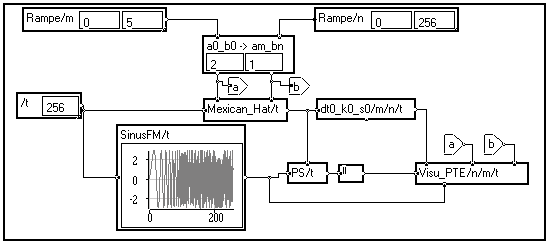
qui donne le résultat suivant en résolution vraie :
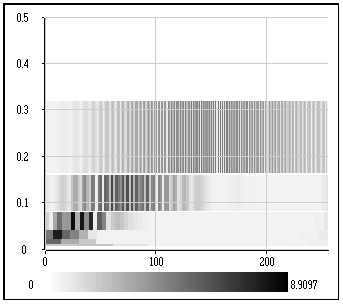
Remarquez que, dans la figure ci-dessus, la partie haute fréquence du signal (au dessus de 0.3 Hz environ) n'est pas couverte. Si l'on souhaite une description complète du signal, il faut considérer une échelle plus petite en faisant varier l'entier m entre -1 et 5 plutôt qu'entre 0 et 5.
La Transformée Continue en Ondelettes (T.C.O.) permet de décomposer un signal selon une collection de signaux (les ondelettes), déduits d'une ondelette mère par des opérations de translations et de dilatation. Chaque type d'ondelette mère possède ses caractéristiques propres (forme, régularité, moments nuls, extension temps-fréquence, etc). On choisira donc telle ou telle ondelette de référence en fonction de ce que l'on veut mettre en valeur dans le signal.
Pour chaque ondelette considérée, à une échelle et à un moment donnés, on calcule le produit scalaire avec le signal. Cela revient en fait à projeter le signal sur l'ondelette. La valeur du produit scalaire ainsi calculé peut donc être vue comme une mesure de la ressemblance entre le signal et l'ondelette.
En choisissant judicieusement les valeurs d'échelle et de décalages, on peut obtenir une description du signal en minimisant la redondance d'information.
L'ensemble des produits scalaires calculés est souvent représenté sous la forme d'un diagramme tridimensionnel qui met en valeur l'éventuel caractère non stationnaire du signal.
1.3. Transformée Inverse Continue en Ondelettes (T.I.C.O.)
1.3.1. Pourquoi une transformée inverse ?
La transformée directe permet d'analyser un signal afin de détecter des singularités ou bien un comportement non stationnaire ou fractal. Il est possible, à partir de l'ensemble des coefficients calculés, de reconstruire le signal de départ.
Bien entendu, s'il s'agit de décomposer le signal puis de le reconstruire immédiatement, cela présente peu d'intérêt ! Mais comme nous l'avons déjà signalé, la phase de reconstruction est le plus souvent précédée d'une phase de modification ou de seuillage des coefficients, à des fins de compression ou de débruitage. L'algorithme de reconstruction est la Transformée en Ondelettes Inverse.
1.3.2. Expression de la transformée inverse
Les coefficients d'ondelettes Ca,b ont été obtenus en projetant le signal x(t) sur la collection d'ondelettes y ab(t). On peut donc considérer la suite des coefficients comme les coordonnées de x(t) dans l'espace formé par les fonctions y ab(t). Par conséquent, le signal s'exprime par :
![]()
Il est donc facile, connaissant les coefficients Ca,b et l'ondelette de référence y (t), de reconstruire le signal x(t).
La macro qui permet de reconstruire le signal à partir des coefficients d'ondelettes issus d'une T.C.O. et de la collection d'ondelettes coorespondante est la suivante :
![]()
On peut partir de l'exemple précédent et reconstruire le signal immédiatement après sa décomposition :
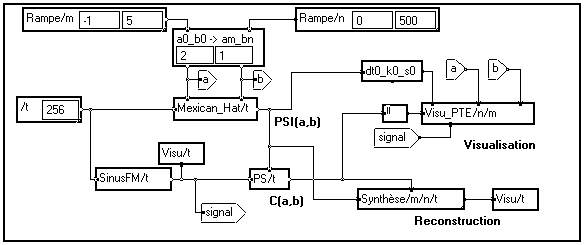
Le signal analysé est toujours la même modulation de fréquence :
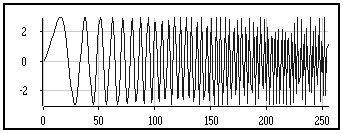
Vérifions que la suite des facteurs d'échelle et des décalages permet de couvrir la totalité du plan temps-fréquence, car dans le cas contraire la reconstruction ne serait pas satisfaisante :
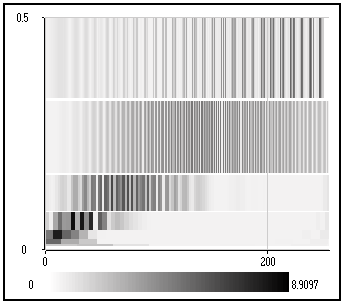
On obtient alors le signal reconstruit à partir de ces coefficients d'ondelettes :
D'autres exemples, comprenant en outre un seuillage des coefficients d'ondelettes, seront présentés dans un chapitre ultérieur.
II. La Transformée en Ondelettes Discrète
La Transformée Continue en Ondelettes décompose un signal selon un ensemble d'ondelettes déduites d'une ondelette de référence par des opérations de dilatation et de translation. L'utilisateur peut choisir ses jeux de facteurs de dilatation et de décalages de façon libre.
Cependant, il est possible d'augmenter l'efficacité de la décomposition, c'est-à-dire de limiter le nombre de facteurs d'échelle à utiliser tout en conservant la même précision dans la décomposition. Nous avons déjà évoqué ce point au chapitre précédent en soulignant l'intérêt de choisir des facteurs d'échelle formés de puissances de 2 (décomposition dyadique).
La Transformée en Ondelettes Discrète (T.O.D.) part de cette considération pour aboutir à un algorithme particulièrement efficace, qui peut se comprendre facilement de manière intuitive.
2.1. Notion de détails et d'approximation
Le principe de base de la T.O.D. est de séparer le signal en deux composantes, l'une représentant l'allure générale du signal, l'autre représentant ses détails. L'allure générale d'une fonction est représentée par ses basses fréquences, les détails par ses hautes fréquences.
Pour séparer les deux, nous avons donc besoin d'une paire de filtres : un filtre passe-bas pour obtenir l'allure générale (aussi appelée approximation ou moyenne), et un filtre passe-haut pour estimer ses détails, c'est-à-dire les éléments qui varient rapidement. Pour ne pas perdre d'information, ces deux filtres doivent bien sûr être complémentaires : les fréquences coupées par l'un doivent être conservées par l'autre. On dit que les deux filtres forment une paire de filtres miroirs en quadrature.
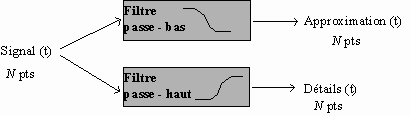
Si nous nous arrêtons là, nous multiplions par 2 la quantité d'information. En effet, si le signal à traiter possède N points, le signal d'approximation et le signal de détails feront également N points chacun, soit 2.N en tout !
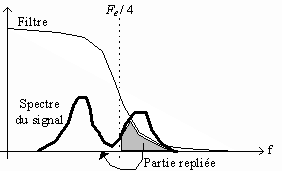
Pour y remédier, le filtre passe-bas est choisi de telle sorte que sa fréquence de coupure soit Fe / 4, où Fe est la fréquence d'échantillonnage du signal. Un filtre passe-haut orthogonal au filtre passe-bas, peut être calculé facilement. En sous-échantillonnant d'un facteur 2 chaque signal, i.e. le signal d'approximation et le signal de détails, on se ramène à deux signaux de longueur N / 2, soit N points en tout : pas de changement dans la quantité d'information.
Intuitivement, nous pouvons justifier ce sous-échantillonnage par le fait que nous avons préalablement filtré le signal avec un filtre de fréquence de coupure Fe / 4. Si le filtre est parfait (filtre en échelon), cela ne pose aucun problème.
En pratique, les filtres utilisés ne sont pas parfaits. L'opération de sous-échantillonnage introduit du repliement : si le signal filtré contient encore un peu d'énergie au delà de Fe / 4, cette énergie est "repliée" dans la bande [0,Fe/4] au moment du sous-échantillonnage et pollue le signal.
Une étape élémentaire de la T.O.D. peut donc se schématiser de la façon suivante :
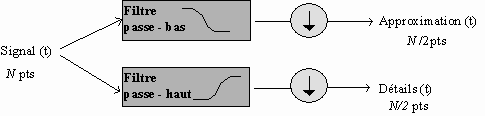
où le symbole ![]() représente l'opération de sous-échantillonnage : on ne prend qu'un point du signal sur deux.
représente l'opération de sous-échantillonnage : on ne prend qu'un point du signal sur deux.
Lien entre l'ondelette et le filtre
A chaque paire de filtres en quadrature est associée une ondelette y (t) et une fonction d'échelle j (t). L'ondelette est une fonction oscillante qui permet de rendre compte des détails du signal. La fonction d'échelle est une fonction plus basse fréquence, associée à l'approximation du signal.
Exemple
Dans l'exemple ci-dessous, on utilise un filtre passe-bas particulier, le filtre "Daubechies 2", qui comporte 4 coefficients. Le signal original, de longueur 512 points, est transformé en deux signaux de 256 points :
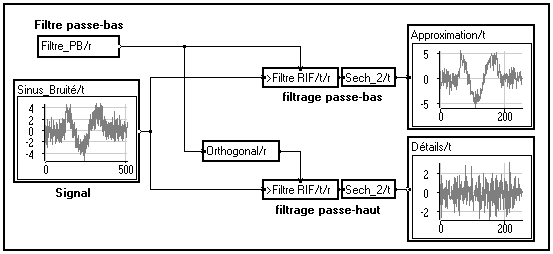
Où sont les coefficients ?
En réalisant une étape élémentaire de la T.O.D., nous obtenons un signal d'approximation et un signal de détails. Les échantillons des signaux de détails sont appelés coefficients d'ondelettes du signal relativement à la décomposition effectuée (ici une décomposition selon l'ondelette "Daubechies 2").
Signalons un abus de langage courant : en principe, seuls les échantillons des signaux de détails devraient être appelés ainsi. Les échantillons du signal d'approximation devraient être appelés "coefficients de fonction d'échelle" (terminologie que nous expliquerons plus loin). Par abus de langage on appelle souvent "coefficients d'ondelettes" l'intégralité des échantillons obtenus (approximation et détails).
Une paire de filtres complémentaires, l'un passe-bas et l'autre passe-haut, permet de transformer un signal de longueur N en deux signaux de longueur N/2 : l'un représentant la tendance du signal et appelée approximation, l'autre représentant ses détails. On dit que l'on est passé à une résolution inférieure.
Pourquoi s'arrêter en si bon chemin ? L'approximation est bien une version lissée du signal de départ, mais elle comporte encore du bruit. Rien ne nous empêche de répéter l'opération de filtrage sur le signal d'approximation, afin d'accéder à une résolution encore inférieure, et ainsi de suite. On obtient alors une décomposition que l'on peut schématiser comme suit :
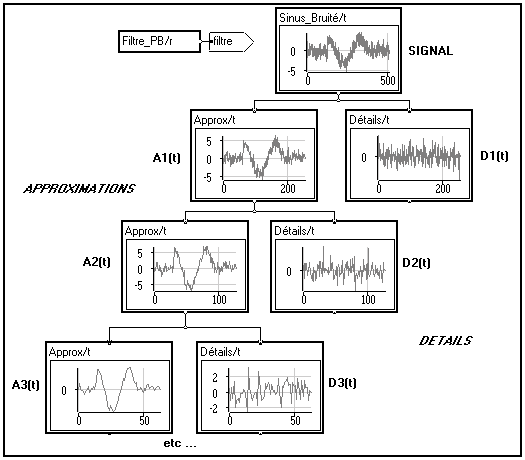
Notez bien que, pour la T.O.D. seuls les signaux d'approximation sont à nouveau décomposés. Les signaux de détails issus du filtrage passe-haut sont laissés de côté à chaque pas.
A chaque itération, on divise la résolution par 2. C'est la raison pour laquelle cette méthode est appelée analyse multirésolution.
Après la jième itération, la longueur du signal d'approximation Aj(t) et du signal de détails Dj(t) est de N / 2j (N étant la longueur du signal de départ).
Jusqu'où aller ?
On pourrait poursuivre cet algorithme en cascade jusqu'à obtenir une seule valeur pour l'approximation et donc aussi une seule valeur pour les détails. En pratique, on pourra parfois s'arrêter avant, tout dépend de l'application envisagée. Nous reviendrons sur ce point ultérieurement. La valeur jmax atteinte, c'est-à-dire le nombre d'itérations effectuées, est appelée niveau de décomposition.
On obtient un signal d'approximation de longueur N / 2jmax et jmax signaux de détails de longueur N / 2 à N / 2jmax, qui forment un jeu de coefficients d'ondelettes.
Comme pour la transformée continue en ondelettes, il est intéressant pour de nombreuses applications de pouvoir reconstruire le signal à partir des coefficients d'ondelettes (i.e. les signaux d'approximation et de détails). Cette opération est appelée reconstruction ou synthèse.
En fait, il est inutile de garder la trace de tous les signaux d'approximation Aj. On peut synthétiser le signal en ne considérant que le signal d'approximation Ajmax au dernier niveau de décomposition et tous les signaux de détails Dj produits à chaque itération. On notera que la somme des longueurs de ces signaux nécessaires à la reconstruction est exactement N, la longueur du signal de départ. Cela signifie que quelque soit le niveau de décomposition atteint, l'information n'est pas redondante.
On se doute qu'il va falloir à nouveau filtrer chaque signal (approximation et détails) puis recombiner approximation et détails. Cependant, nous disposons de signaux de longueur variable de façon dyadique N/2, N/4, N/8, N/16, etc.
Comment revenir à un signal de longueur N ? Tout simplement en sur-échantillonnant le signal d'un facteur 2 à chaque itération, avant l'opération de filtrage. Pour cela, il suffit de doubler à chaque pas la longueur de l'approximation et du détail en introduisant un zéro entre chaque échantillon.
On passe donc de l'approximation Aj à l'approximation Aj-1 par l'opération suivante :
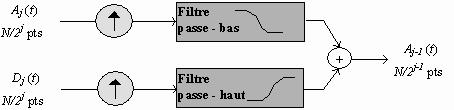
où le symbole ![]() représente l'opération qui consiste à insérer un zéro entre chaque échantillon afin de doubler sa longueur.
représente l'opération qui consiste à insérer un zéro entre chaque échantillon afin de doubler sa longueur.
Pour reconstruire le signal original à partir d'un niveau de décomposition donné, il suffit d'itérer cette suite d'opérations de sur-échantillonnage / filtrage. On reconstruit ainsi récursivement tous les signaux d'approximation à partir du signal d'approximation à la résolution inférieure et du signal de détails :
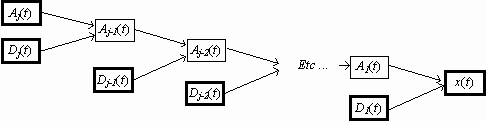
Que devient le repliement ?
L'opération de décomposition du signal en détails et approximations a introduit du repliement. En choisissant judicieusement les filtres passe-haut et passe-bas utilisés pour la synthèse, on peut éliminer ce repliement au moment de la reconstruction. Les filtres de synthèse pourront donc être différents de ceux utilisés pour la décomposition du signal.
2.4. Le problème des effets de bord
Qu'il s'agisse de décomposer un signal ou bien de le reconstruire, nous sommes amenés à filtrer des signaux de longueur finie. L'opération de filtrage consiste à calculer pour chaque échantillon une moyenne pondérée sur un nombre de voisins égal à la longueur de la réponse impulsionnelle du filtre.
Ainsi, partant d'un signal x(n) de N échantillons, on obtient le signal y(n) filtré par le filtre A = [a0, a1, ..., aM-1] de la manière suivante :
![]()
M est la longueur de la réponse impulsionnelle du filtre et offset un entier relatif définissant le centrage du filtre A : si offset = -M / 2, le filtre est dit centré.
On voit tout de suite que l'opération de filtrage va poser un problème aux extrémités du signal, c'est-à-dire lorsque la somme n+k+offset sera soit inférieure à 0, soit supérieure à N-1 : les échantillons correspondants n'existent pas !
Pour remédier à ce problème, il suffit d'étendre le signal de part et d'autre de son intervalle de définition [ n=0 ; n=N-1 ]. Plusieurs approches sont possibles, la bibliothèque Ondelettes de Mustig propose quatre méthodes :
Zero-padding
Cette approche est naïve mais simple à mettre en œuvre : elle consiste tout simplement à supposer que tous les échantillons sont nuls en dehors de l'intervalle de définition du signal :
x( n < 0 ) = x( n > N-1 ) = 0
Si les valeurs du signal à ses extrémités sont très différentes de 0, l'opération introduit des discontinuités qui se propagent à chaque itération.
Périodisation
On suppose que le signal dans son ensemble se reproduit identique à lui-même :
x(-1) = x(N-1) , x(-2) = x(N-2) , x(-3) = x(N-3), etc...
x
(N) = x(0) , x(N+1) = x(1) , x(N+2) = x(2), etc...Cette périodisation du signal provoque, dans le domaine spectral, une discrétisation du spectre qui ne gêne pas la transformée en ondelettes. C'est la raison pour laquelle la périodisation est souvent utilisée pour traiter les effets de bords sur des signaux de courte durée. Par contre, si le signal est très différent à chaque extrémité, des discontinuités importantes peuvent apparaître.
Symétrisation
La symétrisation consiste à calculer le signal "miroir" par rapport aux bords :
x(N) = x(N-2) , x(N+1) = x(N-3) , x(N+2) = x(N-4), etc...
x
(-1) = x(1) , x(-2) = x(2) , x(-3) = x(3), etc...Cette opération introduit moins de discontinuités lorsque l'amplitude du signal varie sensiblement entre ses deux extrémités. Cependant, son effet sur le plan spectral peut être complexe.
Expansion
L'expansion consiste à calculer le signal en dehors de l'intervalle de définition de la manière suivante :
x( -n ) = 2 . x( 0 ) - x( n )
x
( M+n-1 ) = 2 . x( M-1 ) - x( M-n-1 )Elle se révèle assez efficace dans les cas où l'amplitude varie beaucoup entre le début et la fin du signal.
Ces quatre opérations de prise en compte des effets de bords sont schématisées ci-dessous, avec une rampe comme signal d'entrée :
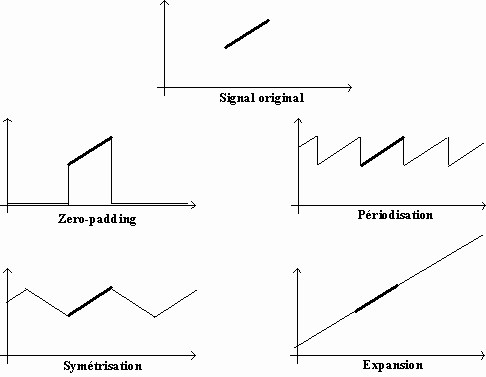
Ces extensions de part et d'autre de l'intervalle de définition sont réalisées à chaque itération de la transformée en ondelettes directe ou inverse.
2.5. Transformée rapide ou Fast Wavelet Transform
L'algorithme de décomposition multirésolution est itératif : chaque signal d'approximation calculé est à son tour décomposé en approximation et détails. Un tel algorithme serait facilement programmable en langage MUSTIG au moyen d'une clôture bouclée et des modules de filtrage et de sous-échantillonnage.
Cependant, il est plus avantageux d'utiliser une méthode plus rapide, connue sous le nom de Transformée en Ondelettes Rapide (T.O.R.). Le terme anglais Fast Wavelet Transform et son abréviation FWT sous toutefois plus usités dans la littérature.
Cet algorithme a été programmé en C en interfacé avec MUSTIG. La gestion des effets de bords est incluse dans le programme en C. Tous les paramètres de la transformée sont facilement réglables depuis MUSTIG.
Le module d'appel à l'externe nécessite certains paramètres d'entrée :
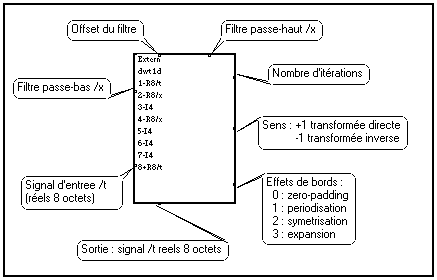
Pour rendre son utilisation plus pratique, ce module est intégré à une macro plus conviviale qui permet d'ajuster facilement les paramètres à l'aide de la souris. La macro correspondante est :
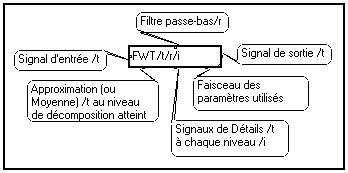
En double-cliquant sur la macro
FWT, vous pouvez faire apparaître les paramètres de réglage :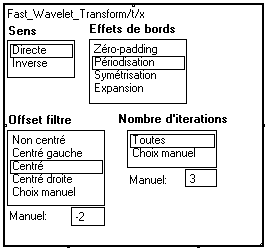
Pour modifier un paramètre, cliquez sur l'option correspondante (la sélection reste encadrée en permanence). Pour l'offset du filtre et le nombre d'itérations, vous pouvez entrer une valeur numérique, elle sera prise en compte lorsque vous sélectionnerez "Choix manuel". Ces paramètres sont communiqués sur la borne inférieure droite sous la forme d'un faisceau (ou bus), afin de pouvoir être réutilisés dans la suite du traitement :
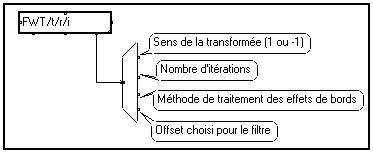
Le module
DWT1D/t/r situé dans "Modules Elémentaires Transformée Discrète" permet en effet de réaliser une transformée en ondelettes discrète en entrant le faisceau des paramètres sur sa borne inférieure. Le faisceau peut être modifié à l'aide des modules suivants :Change_sens : Changement du sens de la transformée
(directe ¬ ® inverse)
Ajuste_offset/r : Modification de l'offset du filtre pour assurer une bonne
reconstruction du signal après transformée inverse.
Il est ainsi possible de réaliser une transformée directe, puis une transformée inverse avec les mêmes paramètres, en changeant uniquement le sens de la transformée.
Vous pouvez construire vous-même ce faisceau de paramètres à partir d'une interface utilisateur grâce au module
Parametres/t/r. Pour des exemples d'utilisation de ces modules élémentaires, voir par exemple l'utilitaire de débruitage DEBRUITAGE/t ou les exemples fournis (liste en fin de volume).
2.5.2. Disposition des coefficients d'ondelettes
Si on présente en entrée du module
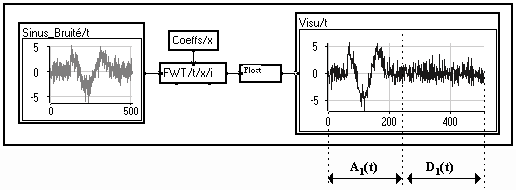
FWT un signal x(n) de longueur N échantillons, on obtient en sortie un signal de même longueur comprenant de gauche à droite :
Exemple pour une seule itération
Exemple pour deux itérations

Et ainsi de suite... Si toutes les itérations sont effectuées, tous les échantillons du signal de sortie sont des coefficients d'ondelettes (i.e. des détails) à l'exception du premier qui représente la moyenne du signal.
2.5.3. Séparation de l'approximation et des différents niveaux de détails
Par commodité, l'approximation obtenue au dernier niveau de décomposition jmax est présentée selon la variable /
t sur la borne inférieure gauche du module FWT. Les différents coefficients sont présentés sur la borne inférieure droite selon les variables /t et /i (i représentant le niveau de décomposition). Vous pouvez visualiser facilement chaque niveau de détails grâce au module de sortie VisuNv/t/i de la bibliothèque standard V4.0, qui accepte les variables dynamiques. Dans l'exemple ci-dessus on obtient :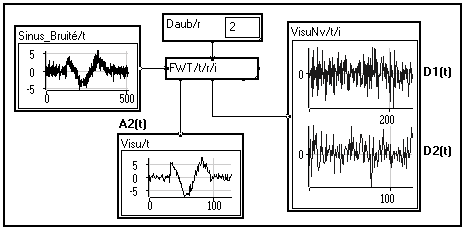
Cette séparation de l'approximation et des différents niveaux de détails vous permet de visualiser et de traiter chaque niveau séparément.
2.5.5. Mise en œuvre de la transformée inverse
Le module MUSTIG est le même que celui utilisé pour la transformée directe, mais les signaux disponibles sur les bornes inférieures n'ont bien sûr aucun sens dans le cas de la transformée inverse.
Le jeu de coefficients dont on souhaite calculer la transformée en ondelettes inverse doit être présentée à l'entrée du module
FWT avec la même structure que le signal produit lors de la transformée directe : d'abord le signal d'approximation, puis les différents signaux de détails par ordre décroissant de niveau de décomposition.
Exemple avec 2 itérations dans chaque module
FWT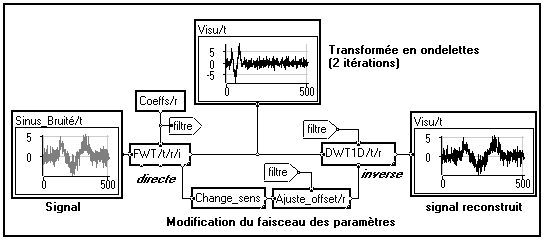
Notez l'utilisation d'un report ("filtre") pour alléger le graphe. Les paramètres utilisés pour la transformée directe sont captés sur la borne inférieure droite du module intégré de transformation
FWT et transmis au module élémentaire de DWT1D afin que la transformée inverse soit réalisée avec les mêmes paramètres (même méthode de traitement des effets de bords, même nombre d'itérations). Le module élémentaire Change_sens permet de passer d'une transformée directe à une transformée inverse. Le module élémentaire Ajuste_offset modifie d'offset du filtre afin que la reconstruction soit parfaite.
Si, au lieu de traiter le signal en sortie droite du module
FWT, vous avez utilisé les bornes inférieures (séparation des coefficients d'approximation et de détails), pour effectuer un seuillage par exemple, il faut reconstruire un vecteur de structure correcte à partir de l'approximation et des différents niveaux de détails. Pour cela, utiliser le module suivant :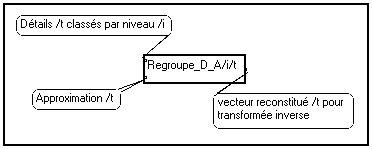
Exemple
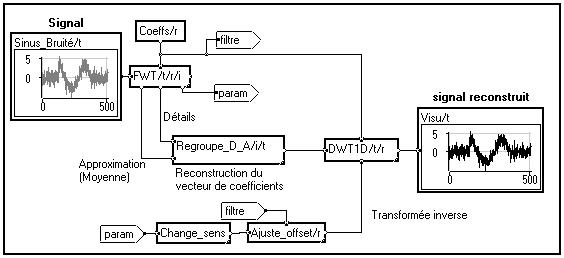
Remarque
Là encore, les mêmes paramètres sont utilisés pour les transformée directe et inverse grâce à l'utilisation du faisceau de paramètres. Un report ("param") a été utilisé pour alléger le graphe. Le sens de la transformée est inversée par le module
Change_sens, et l'offset du filtre est ajusté par le module Ajuste_offset. Les applications intégrées telles que les modules de débruitage réalisent ces opérations automatiquement, et incorporent des modules de seuillage des coefficients à des fins de débruitage ou de compression.
2.6. A quoi ressemblent les ondelettes et les fonctions d'échelle ?
Nous avons parlé de filtres, de sous-échantillonnage, de détails, d'approximations, mais nous n'avons pas encore pu voir l'allure des fonctions d'ondelettes que nous pouvons utiliser. En fait, ces ondelettes n'ont pas en général d'expression analytique. Il est d'ailleurs inutile de les calculer explicitement : le filtre suffit à calculer la transformée.
Nous pouvons cependant synthétiser les ondelettes correspondant à un filtre donné au moyen de la transformée en ondelettes inverse. Sachant que la transformée d'une ondelette y (t) (PSI) est un pic de Dirac, il suffit de calculer la transformée inverse d'un Dirac pour observer l'ondelette.
La position du Dirac présenté en entrée de la transformée en ondelette inverse conditionne l'échelle de l'ondelette obtenue : plus le Dirac est proche du début du signal (zone des basses résolutions dans la transformée en ondelette rapide), plus l'échelle de l'ondelette sera grande (i.e. plus l'ondelette sera "étalée"). Le module
Filtre->PSI/t/r vous permet d'estimer l'ondelette à une échelle donnée.
Exemple
Visualisation de la forme de l'ondelette "Daubechies 2". Elle présente la propriété d'être de nature fractale :
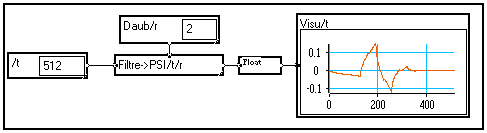
D'autres formes d'ondelettes seront présentés plus loin. La visualisation de l'ondelette y (t) permet d'évaluer rapidement ses propriétés : estimation de son étendue, de son spectre, de sa régularité, etc.
Il faut simplement veiller à ce que la position du Dirac soit supérieure à l'ordre du filtre, sinon la totalité de l'ondelette ne sera pas visible. De même, la reconstruction du signal faisant appel à une segmentation dyadique, il convient de ne pas choisir une position trop proche d'une puissance de deux si on souhaite limiter les effets de bords.
2.7. Analyse multirésolution à 2 dimensions
Jusqu'ici nous n'avons considéré que la transformation en ondelettes de signaux mono-dimensionnels. Il est bien entendu possible de calculer la transformée d'un signal à deux dimensions (i.e. une image ou une matrice), et plus généralement celle d'un signal à D dimensions (mais si D>2 la visualisation des résultats est plus difficile).
La transformée en ondelettes discrète d'un signal à deux dimensions x et y peut être calculée de manière simple par la méthode de séparabilité du noyau. Cette méthode consiste tout simplement, à chaque itération, à transformer l'image successivement selon chaque dimension x et y. Comme pour le cas monodimensionnel, la taille de l'image à traiter est divisée par 4 à chaque itération (par 2 selon chaque dimension).
Concrètement, l'algorithme à suivre pour calculer la transformée en ondelettes discrète d'une image de taille NxN est le suivant :
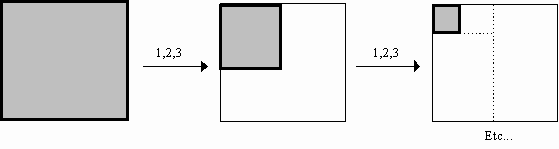
Nous retrouvons donc le même principe que l'analyse multirésolution 1D : faire une étape de décomposition, garder une partie du signal (les détails) pour plus tard, puis recommencer la décomposition sur l'autre partie (l'approximation).
Le module MUSTIG qui vous permet d'effectuer cette décomposition à deux dimensions est le suivant :
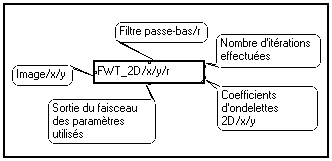
Il s'agit d'une simple adaptation du module de transformée en ondelettes à une dimension : une boucle permet de découper la partie de l'image à traiter à chaque itération. La transformée proprement dite est toujours assurée par l'externe en C. Bien entendu, les transformations selon chaque dimension sont réalisées avec les mêmes paramètres (offset, traitement des effets de bords, sens, nombre d'itérations), de telle sorte que l'ensemble soit homogène.
Les paramètres de réglage sont les mêmes que pour le cas à une dimension : sens de la transformée, offset du filtre, méthode de traitement des effets de bords et nombre d'itérations à réaliser. Ils peuvent être visualisés et modifiés et double-cliquant sur le module
FWT_2D. Ils sont présentés sur la borne inférieure en un faisceau (cf. paragraphe 2.5.1).Comme pour la transformée à une dimension, le module élémentaire
Parametres permet de construire ce faisceau à l'aide de clic souris. Le module élémentaire DWT2D/x/y/r permet de réaliser une transformée en ondelettes bidimensionnelle en passant directement le faisceau de paramètres. Cela permet par exemple de réaliser une transformée 2D inverse avec les mêmes paramètres que ceux utilisés pour la transformée directe (cf. paragraphe 2.5.5 et utilitaire DEBRUITAGE_2D fourni).Enfin, le nombre d'itérations effectuées en communiqué en sortie droite supérieure car de nombreux modules de traitement des coefficients 2D ont besoin de connaître ce paramètre.
2.7.3. Interprétation des résultats
Les détails renvoient à la même notion que pour un signal 1D : ils représentent les variations haute fréquence d'une image (transitions entre zones de contrastes différents, parties plus ou moins texturées, etc).
La particularité de la transformation que nous venons de décrire est sa directivité. C'est-à-dire que la transformée en ondelettes bidimensionnelle sépare à chaque itération (i.e. pour chaque échelle) :
Après avoir effectué jmax itérations sur une image M(x,y) de taille NxN, on obtient :

Exemple sur une image test
Construisons le petit programme suivant :
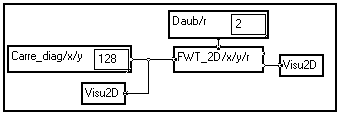
Choisissons, pour simplifier, de faire trois itérations. La figure ci-dessous représente l'image originale et sa transformée 2D :


L'image originale a bien été décomposée en une image approximation de taille 32x32, et trois séries de trois images de taille 128x128, 64x64 et 32x32, qui représentent les détails horizontaux, verticaux et diagonaux pour chaque niveau de décomposition.
Notons que, comme dans le cas de signaux à une dimension, la taille totale de l'image résultat est la même que celle de l'image originale : il n'y a ni perte d'information, ni redondance.
La transformée inverse s'obtient avec le même module
FWT_2D, simplement en choisissant l'option "Inverse" dans la face de réglage des paramètres. Elle permet de reconstruire l'image originale à partir des coefficients issus de la transformée discrète 2D.De même, il est nécessaire pour reconstruire l'image d'effectuer un nombre d'itérations identique à celui effectué lors de sa décomposition. Pour en être assuré, utilisez le faisceau de paramètres transmis sur la borne inférieure du module
FWT_2D et communiquer les paramètres au module DWT2D après avoir inversé le sens de la transformée à l'aide du module Change_sens (cf. paragraphe 2.5.5).Attention cependant à l'offset du filtre : une reconstruction parfaite peut nécessiter un offset différent à la décomposition et à la reconstruction. Comme pour la cas à une dimension, le module
Ajuste_offset vous permettent de réaliser cette opération.Des exemples de décomposition / reconstruction d'images sont proposés notamment dans le module
DEBRUITAGE_2D et les exemples fournis.
2.7.5. Allure des ondelettes 2D
On peut visualiser les ondelettes à deux dimensions en procédant comme à une dimension : il suffit de calculer la transformée inverse d'un Dirac à deux dimensions.
Exemple
Le programme suivant permet de visualiser l'ondelette "Daubechies 2" bidimensionnelle :
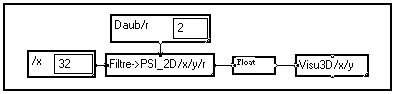
Le résultat de la macro
Visu3D est représenté ci-dessous :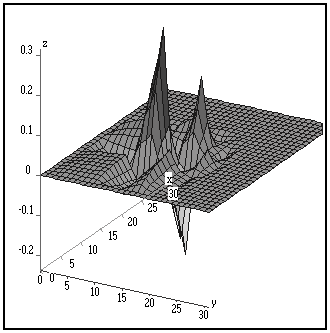
En changeant la position du Dirac, on peut modifier la position et l'échelle de l'ondelette.
Dans cette partie nous avons mis en œuvre des algorithmes de décomposition multirésolution de signaux 1D et 2D, ainsi que des algorithmes de reconstruction (synthèse). Nous avons vu comment visualiser les ondelettes correspondant à un filtre donné, à une et deux dimensions.
L'analyse multirésolution permet de séparer les détails d'un signal à plusieurs résolutions données, ces résolutions variant avec un pas dyadique. Le but est bien entendu de traiter les coefficients de détails avant de procéder à la reconstruction.
III. Algorithmes de seuillage des coefficients
Nous savons mettre en œuvre une décomposition et une synthèse en ondelettes soit continue, soit discrète. Sauf à des fins d'analyse ou pédagogiques, il est évident qu'on ne décompose pas un signal ou une image pour le seul plaisir de la reconstruire à l'identique ! Nous allons maintenant aborder les différentes manières dont on peut modifier les coefficients d'ondelettes à des fins de compression ou de débruitage.
Les coefficients d'ondelettes correspondent aux détails d'un signal ou d'une image. Lorsqu'un détail est faible, il peut être ignoré sans que cela affecte les données de manière visible. Le seuillage des coefficients d'ondelettes est donc un bon moyen d'éliminer les détails les plus faibles, que l'on considère comme du bruit. On peut dégager deux grandes applications de ce principe :
Concrètement, on procède de la manière suivante que l'on soit à une ou deux dimensions :
Méthodologie
Attention : Avant de mettre en place une méthode de seuillage des coefficients, nous vous conseillons fortement de vérifier que la reconstruction est parfaite avec l'intégralité des coefficients d'ondelettes. En effet, les effets de bords ainsi qu'un mauvais centrage des filtres peuvent produire une reconstruction imparfaite même en l'absence de seuillage. Concrètement, nous vous recommandons la procédure suivante :
Il existe plusieurs méthodes de seuillage des coefficients, que nous allons maintenant décrire.
3.2. Seuillage brut ou "hard thresholding"
Le principe du seuillage brut est simple. On commence par se fixer un seuil l >0. Si la valeur absolue d'un coefficient d'ondelette donné d est supérieure à l , on garde ce coefficient tel quel. Sinon, on le met à zéro :
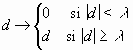
Nous verrons plus loin comment déterminer le seuil l . On peut schématiser cette transformation comme suit :
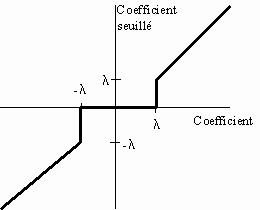
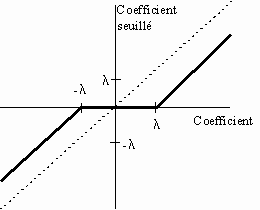
3.3. Rétrécissement ou "soft thresholding" ou "shrinkage"
Plutôt que de simplement "conserver ou tuer" un coefficient, le rétrécissement propose d'appliquer à chaque coefficient la transformation suivante :
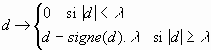
qui permet de seuiller les coefficients de manière plus "douce" :
3.4. Détermination du seuil à utiliser
On connaît (ou on détermine par tâtonnements) la valeur l à utiliser. C'est bien sûr le cas le plus simple, mais pas le plus fréquent ni le plus réaliste !
On définit la valeur du seuil l comme une fraction de la valeur absolue du plus grand coefficient. Par exemple, on choisit d'éliminer tous les coefficients dont la valeur absolue est inférieure à s = 50% de la valeur absolue du coefficient le plus grand :
![]()
Vous pouvez bien sûr utiliser les possibilités multidimensionnelles de MUSTIG pour tester plusieurs valeurs du seuil absolu ou relatif (cf. paragraphe 3.9).
3.4.4. Seuil quantitatif absolu
Si on connaît le nombre N de coefficients d'ondelettes issus de la transformée directe, on peut choisir directement le nombre N' de coefficients que l'on veut conserver. Dans ce cas, on garde les N' plus grands coefficients, et on met tous les autres à zéro. Cette sélection est réalisée en classant d'abord les coefficients par ordre décroissant de valeur absolue, puis en sélectionnant les N' plus grands. La valeur du dernier coefficient donne le seuil à utiliser.
Attention : l'opération de classement d'un grand nombre de coefficients est lente, même avec une méthode de tri rapide. Dans le cas d'images, il peut être plus intéressant d'effectuer un seuillage absolu ou relatif en réglant le seuil par tâtonnements et en estimant l'efficacité du seuillage à chaque pas (cf. paragraphe 3.7).
3.4.4. Seuil quantitatif relatif
C'est la méthode la plus intuitive : on choisit de ne conserver que s % du nombre total de coefficients (les plus grands en valeur absolue bien sûr !). La valeur du seuil l est donc déterminée par classement dans l'ordre décroissant des coefficients, de telle sorte qu'il ne reste plus que le pourcentage souhaité.
Si N est le nombre de coefficients à seuiller et N' le nombre de coefficients non nuls après seuillage, on a :
![]()
Cette méthode est très utilisée car la valeur de s est directement liée au taux de compression. Par exemple si s = 50, on ne garde que la moitié des coefficients, donc le taux de compression est voisin de 2 (en omettant les positions des coefficients). Si s = 25, on garde le quart des coefficients avec un taux de compression égal à 4.
Attention : l'opération de classement d'un grand nombre de coefficients est lente, même avec une méthode de tri rapide. Dans le cas d'images, il peut être plus intéressant d'effectuer un seuillage absolu ou relatif en réglant le seuil par tâtonnements et en estimant l'efficacité du seuillage à chaque pas (cf. paragraphe 3.7).
3.4.5. Seuil universel ou "seuil de Donoho"
Donoho et Johnston proposent, pour seuiller un jeu de N coefficients, d'utiliser la valeur suivante (en seuillage brut ou en rétrécissement) pour le seuil l :
![]()
où s est ici un facteur qui représente la variance du bruit. On peut montrer que cette méthode permet de minimiser la différence entre le signal reconstruit et le signal original.
3.5. Modules MUSTIG de seuillage des coefficients
Toutes les méthodes décrites plus haut sont proposées dans la bibliothèque Ondelettes :
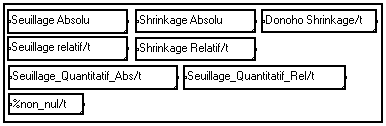
3.6. Comment séparer et seuiller les coefficients ?
La méthode du seuillage absolu ne nécessite aucun examen préalable de la liste des coefficients. Elle peut donc être utilisée quelque soit le nombre de dimensions de la collection de coefficients de détails.
Les autres méthodes en revanche, nécessitent de parcourir l'intégralité des coefficients pour, selon le cas, rechercher le maximum absolu (seuillage relatif), le nombre de coefficients, ou bien les classer par ordre décroissant (seuillage quantitatif).
Or les coefficients peuvent présenter plusieurs dimensions s'ils ont été séparés par niveau de décomposition :
auxquelles s'ajoutent pour une image :
Afin de pouvoir utiliser les mêmes modules de seuillage quelque soit le nombre de dimensions, il importe de ramener toutes ces données à un vecteur unidimensionnel. C'est-à-dire qu'il faut mettre bout à bout tous les coefficients de façon à ne conserver que la seule variable n.
De plus, le résultat de la transformée en ondelettes contient non seulement les détails, mais aussi l'approximation au niveau de décomposition atteint. Il faut donc isoler les coefficients de détails afin de ne seuiller que ceux là.
Les détails sont directement disponibles, classés par ordre de résolution croissant sur la borne inférieure droite du module de décomposition multirésolution. Ils dépendent de deux variables : la position (t) et le niveau de décomposition (i). La procédure à suivre pour le seuillage est donc :
Différent modules permettent de réaliser chacune de ces étapes. Le graphe MUSTIG correspondant à une opération de seuillage prend la forme suivante :
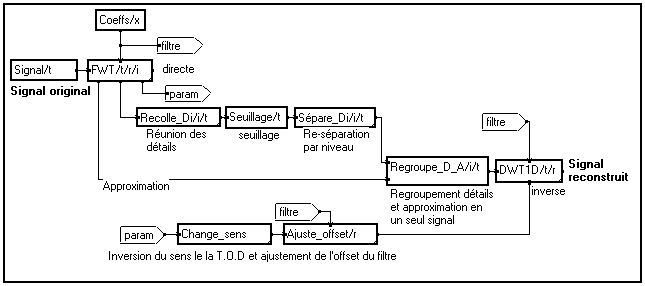
Avec toujours bien sûr le même nombre d'itérations pour les transformées directe et inverse, grâce à l'utilisation du faisceau de paramètres en sortie de
FWT, et communication de ce faisceau au module élémentaire de transformation DWT1D.
En sortie du module
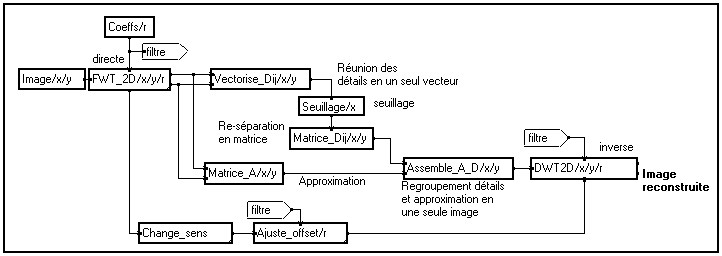
FWT_2D appliqué à une image M(x,y), nous obtenons une image M'(x,y) qui contient à la fois les détails verticaux, horizontaux et diagonaux, et l'approximation.Pour séparer et seuiller les coefficients de détails, il faut donc procéder comme suit :
Quelques modules MUSTIG suffisent à réaliser de façon simple toutes ces opérations. Le seuillage des coefficients de détails dans le cas bidimensionnel prend la forme suivante :
3.7. Comment évaluer l'efficacité du seuillage ?
Afin d'obtenir le meilleur compromis taux de compression / qualité de reconstruction, il importe de pouvoir évaluer rapidement le nombre de coefficients qui ont été annulés par la procédure de seuillage. Une macro MUSTIG a été conçue à cet effet :
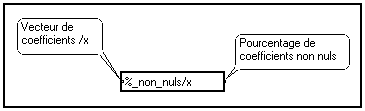
Vous pouvez donc connaître, pour une valeur donnée du seuil, le pourcentage de coefficients qui ont été éliminés.
Dans certains cas, par exemple lorsqu'une image présente un bruit orienté dans une direction préférentielle, on peut envisager de seuiller différemment les détails horizontaux, verticaux et diagonaux d'une image. Pour cela, il faut pouvoir séparer les trois types de détails produits par la transformée en ondelettes, les traiter individuellement, puis reconstruire la matrice de détails globale afin de calculer la transformée inverse.
Pour séparer les détails horizontaux, verticaux et diagonaux, utilisez la macro suivante :
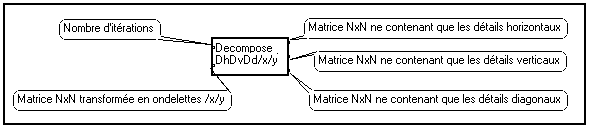
Vous pouvez alors seuiller ou annuler les coefficients selon chaque direction. Pour reconstruire la matrice de détails globale, utilisez la macro :
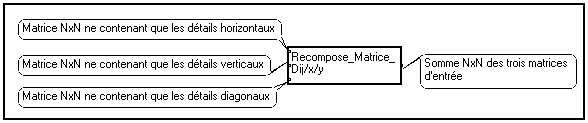
Il suffit alors d'ajouter cette matrice de détails à la matrice d'approximation seule pour obtenir la matrice de transformée en ondelettes seuillée. Le calcul de la transformée inverse donnera l'image traitée. Un exemple de tel traitement est proposé au paragraphe 3.10.
Nous allons utiliser les possibilités multidimensionnelles de MUSTIG pour tester différentes valeurs de seuil. Le signal à débruiter est une modulation linéaire de fréquence bruitée :
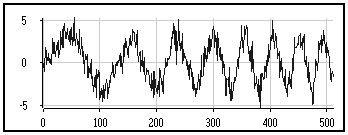
On cherche à enlever le bruit en ne gardant qu'une faible proportion des coefficients de détails. Pour cela, on construit le programme suivant :
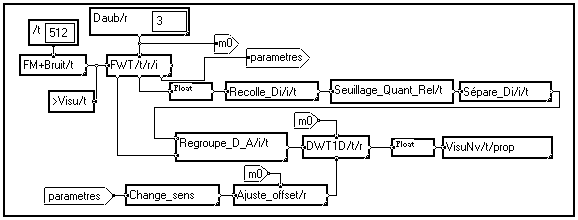
Mais au lieu d'indiquer une seule valeur du seuil dans la macro "
Seuillage_Quant_Rel/t", on entre un vecteur de valeurs selon la variable "/prop", représentant les différentes proportions de seuil que l'on souhaite tester :
Grâce à sa conception capable de prendre automatiquement en compte de nouvelles dimensions, MUSTIG réalise le calcul du signal débruité pour chaque valeur du seuil relatif. On obtient donc en sortie un signal à deux dimensions : le temps t et la proportion de coefficients conservés prop. On peut visualiser le résultat facilement à l'aide par exemple du module de visualisation "
VisuNv/t/prop" :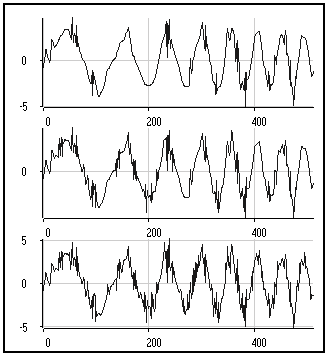
3.10. Exemple à deux dimensions
L'exemple suivant n'a qu'un but pédagogique : il vise à illustrer les différentes manières de traiter les coefficients de détails et ne représente pas un traitement optimal du problème soulevé.
Supposons que l'image à traiter présente un bruit de forte amplitude sous la forme de ligne horizontales :

Dans ce cas, il peut être judicieux de traiter différemment les détails horizontaux, verticaux et diagonaux de la transformée en ondelettes. Le graphe suivant illustre cette possibilité :
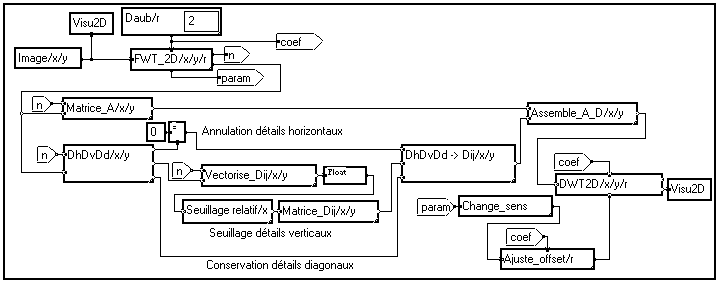
Dans ce traitement, nous avons choisi pour ôter le bruit d'annuler tous les coefficients de détails horizontaux en utilisant le module "
=" qui permet d'étendre la dimension d'un signal. Les coefficients de détails verticaux sont seuillés à l'aide d'une méthode de seuillage relatif, et les coefficients de détails diagonaux sont laissés en l'état.On obtient en sortie de la transformée inverse l'image suivante :

L'image est bien entendu plus floue que l'originale puisque de nombreux détails horizontaux et verticaux ont été enlevés. Cependant, les lignes parasites horizontales ont presque disparu. On peut observer que les détails horizontaux du personnage (bouche, sourcils) sont moins nets que les détails verticaux (main droite, arête du nez). En effet, la totalité des détails horizontaux ont été supprimés, alors que les forts détails verticaux subsistent après le seuillage relatif. Les détails diagonaux (bras gauche, partie gauche de la chevelure) apparaissent bien car les coefficients de détails diagonaux n'ont pas été seuillés.
IV. TRANSFORMEE EN PAQUETS D'ONDELETTES
La décomposition en paquets d'ondelettes est une généralisation de l'analyse multirésolution. Elle consiste à décomposer le signal sur un arbre de fonctions de base obtenues à partir de l'ondelette mère, puis à trouver dans cette librairie une suite d'ondelettes qui remplit les deux conditions suivantes :
Autrement dit, on décompose le signal selon une collection de bases, puis on sélectionne les bases qui minimisent une certaine fonction de coût. Cela permet dans certains cas d'augmenter le taux de compression du signal à résultat équivalent.
Comme pour la décomposition en ondelettes, il s'agit toujours de décomposer un signal au moyen d'un filtre passe-bas et d'un filtre passe-haut complémentaires. La différence réside dans le fait que les différents signaux de détails vont également faire l'objet à chaque itération d'une décomposition selon le même principe. La décomposition en paquets d'ondelettes peut donc être représenté sous la forme d'un arbre binaire :
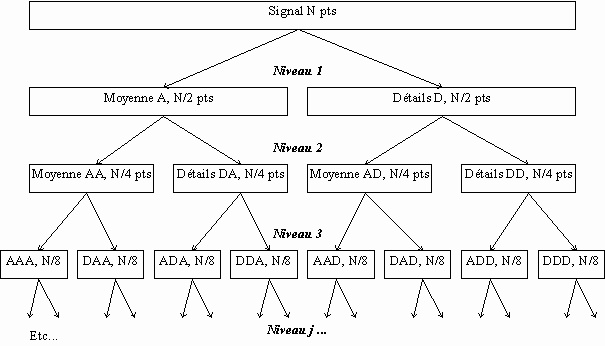
Pour chaque noeud intermédiaire de l'arbre (noeud père), on calcule un signal de moyenne (A) et un signal de détails (D). Deux signaux sont appelés noeuds fils. Chaque fils constitue ensuite un noeud père qui engendre à son tour deux fils, et ainsi de suite.
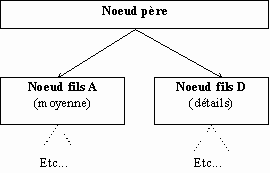
Ainsi, au jième niveau de décomposition, on obtient 2j signaux de longueur N / 2j chacun. Notons que le nombre total de points reste constant d'un niveau de décomposition à l'autre.
Bien sûr, si l'on considère l'ensemble de tous ces signaux, on a une redondance d'information d'un facteur j, ce qui n'est pas très intéressant pour une application comme la compression de données !
Il va donc falloir sélectionner dans cet arbre binaire les noeuds (les signaux) qui satisfont à un certain critère (en l'occurrence la minimisation d'une fonction de coût), de manière à ramener la transformée à un ensemble de N échantillons exactement, que l'on pourra seuiller et inverser comme précédemment.
4.2. Fonctions de coût entropiques
Pour nous ramener à un signal de longueur N exactement, nous pourrions considérer dans l'arbre binaire l'ensemble de toutes les combinaisons qui donnent un signal de longeur N, calculer la transformée en paquets d'ondelettes inverse, et ainsi déterminer la combinaison qui donne le meilleur résultat.
Malheureusement, le nombre de combinaisons envisageables est astronomique dès que la longueur du signal dépasse quelques échantillons ! Par conséquent, nous avons besoin d'un critère qui puisse nous indiquer si tel noeud intermédiaire de l'arbre doit être sélectionné tel quel, ou bien s'il vaut mieux conserver sa moyenne et ses détails. Ce critère est appelé fonction de coût.
Nous allons donc calculer le coût du signal de chaque noeud de l'arbre, puis nous sélectionnerons la combinaison de ces signaux qui donne le coût total minimal.
Il existe différentes manières de calculer le coût d'un signal x(n) de longueur N. Nous proposons dans cette bibliothèque des modules permettant de calculer les plus courantes.
|
Fonction de coût |
Expression |
|
Entropie non normalisée |
|
|
Entropie de Shannon |
|
|
Dimension |
|
|
Compression |
|
|
Proportion supérieure à un seuil absolu |
|
|
Proportion supérieure à un seuil relatif |
|
|
Norme lp |
|
Les modules MUSTIG permettant de réaliser ces calculs sont présentés ci-dessous. Le module
Energie=1/t permet de ramener l'énergie du signal à 1 avant le calcul de la norme lp.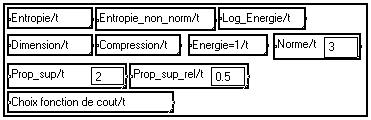
D'autres fonctions de coût existent et peuvent facilement être programmées en langage MUSTIG en cas de besoin. Notons que le coût d'un signal est parfois appelé entropie par abus de langage, même lorsque la fonction utilisée n'est pas l'entropie définie ci-dessus. Le module "
Choix fonction de cout /t" vous permet de choisir entre plusieurs fonctions de coût à l'aide de la souris.
4.3. Sélection de la combinaison de noeuds optimale
Nous savons maintenant calculer le coût du signal correspondant à chaque noeud de l'arbre. Nous pouvons donc sélectionner la combinaison de noeuds qui présente le coût total le plus faible. Il y a plusieurs méthodes pour effectuer cette sélection des noeuds.
4.3.1. Méthode des bases d'ondelettes
Cette méthode correspond à la transformée discrète en ondelettes, telle qu'elle a été exposée dans les chapitres précédents : on garde tels quels tous les noeuds père correspondant à des détails, et on calcule les noeuds fils des signaux de moyenne :
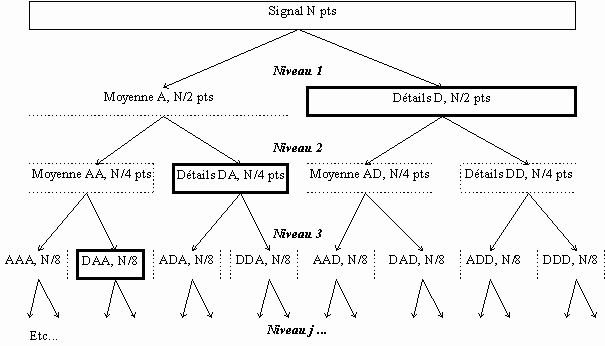
A la fin, on conserve donc un signal de moyenne et plusieurs signaux de détails de longueur décroissante, ce qui correspond bien à une décomposition en ondelettes classique.
Ici, la fonction de coût ne sert donc pas vraiment à sélectionner les noeuds, mais elle permet de connaître le coût total de la transformée, par exemple pour comparer ultérieurement avec d'autres méthodes de sélection. Il est naturellement plus efficace d'utiliser directement le module de transformée discrète en ondelettes pour effectuer cette transformation. C'est pourquoi cette méthode n'a pas été implémentée.
4.3.2. Méthode du meilleur niveau (Best Level)
Dans cette méthode, on calcule le coût total de chaque niveau de décomposition en sommant les coûts des noeuds de ce niveau. On retiendra comme décomposition finale l'ensemble des signaux du niveau de plus faible coût :
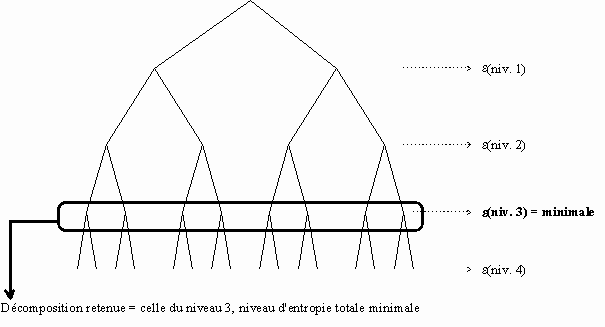
4.3.3. Méthode de la meilleure base (Best Basis)
C'est la méthode qui donne l'entropie totale minimale, c'est donc en général la plus efficace. Au lieu de procéder niveau par niveau, on va considérer chaque noeud de l'arbre binaire individuellement, à partir de l'avant dernier niveau de décomposition, et comparer son coût à la somme des coûts de ses fils.

Si le coût du noeud père est plus faible que celui de ses deux fils réunis, alors la décomposition de ce signal père n'est pas justifiée : on garde le signal père tel quel, et on recommencer avec son propre noeud père au niveau inférieur. En revanche, si le coût total des fils est plus faible, on a intérêt à garder les signaux fils plutôt que le signal père pour diminuer l'entropie totale de la décomposition.
![]()
On obtient donc la combinaison de signaux dont l'entropie totale est la plus faible possible, par exemple :
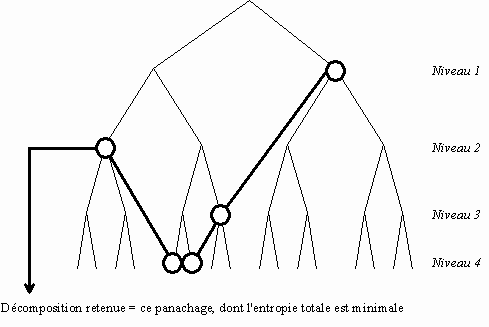
Grâce à la décomposition dyadique des signaux, on est assuré d'obtenir une décomposition finale de longueur exactement N, longueur du signal de départ. Il n'y a donc ni perte ni création d'information. Simplement, le signal a été décomposé selon une sélection de fonctions de base (la décomposition retenue), choisies parmi une collection plus complète (l'arbre binaire en entier), de telle manière que ce choix minimise l'entropie totale du signal décomposé.
Cette sélection sur critère entropique est plus complexe que la décomposition classique en ondelettes, mais puisque l'entropie est en général plus faible, le nombre de coefficients seuillés est généralement plus élevé, d'où un meilleur taux de compression. Attention toutefois : certains signaux comme les modulations linéaires de fréquence sont mal adaptés à la décomposition en paquets d'ondelettes. L'algorithme Meilleure Base peut ne pas donner de très bon résultats sur ces signaux.
4.4. Mise en œuvre sous MUSTIG
4.4.1. Transformée en Paquets d'Ondelettes Directe
La transformée en Paquets d'Ondelettes directe est réalisée au moyen du module
DWPT1D/t/r/rang de la bibliothèque. Ce module transforme un signal incident x(n) de longueur N en NbIter signaux de longueur N, représentant les coefficients de Paquets d'Ondelettes. NbIter est le nombre d'itérations choisi, égal au nombre de niveaux de décomposition. Ce paramètre est réglable à l'intérieur de la macro DWPT/t/r/rang, tout comme la méthode de traitement des effets de bords et le décalage du filtre.
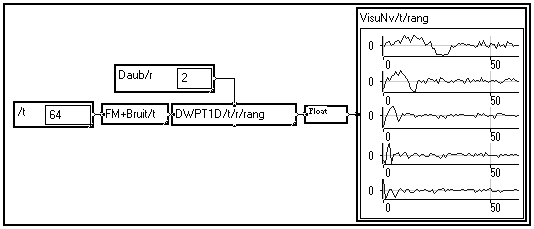
Comme vous pouvez l'observer sur l'exemple ci-dessus, les coefficients en sortie du module sont rangés de manière classique :
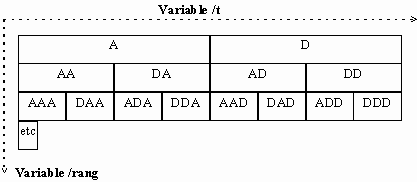
La variable /rang est créée à l'intérieur de la macro en fonction du nombre d'itérations choisi.
Sur la borne inférieure du module de transformée en paquets d'ondelettes directe
DWPT1D, un faisceau à trois bornes est communiqué. Il contient les paramètres utilisés lors de la transformée :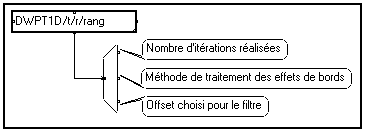
Comme dans le cas de la transformée en ondelettes à une dimension, ce faisceau de paramètre peut être réutilisé dans la suite du traitement. Vous pouvez fabriquer vous-même ce faisceau à l'aide de clics souris en utilisant le module élémentaire
Parametres_wpkt. Vous pouvez effectuer une transformée en paquets d'ondelettes directe en communiquant directement un faisceau de paramètres : utilisez pour cela le module élémentaire DFWPT_1D/t/r/rang.
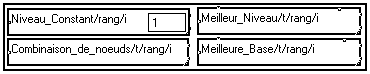
L'information en sortie de la transformée est redondante d'un facteur NbIter, puisque NbIter jeux de N coefficients sont obtenus à partir d'un signal de longueur N. Il faut donc sélectionner un ensemble de N coefficients d'après un critère entropique. Plusieurs méthodes sont proposées dans la boîte "sélection des Niveaux" (cf. Aide en ligne de chaque module) :
|
Nom du module |
Descriptif |
|
Niveau_Constant/rang/i |
Sélection des noeuds de l'arbre à un niveau de décomposition que vous spécifiez vous-même à l'intérieur du module. |
|
Combinaison_de_Noeuds/t/rang/i |
Sélectionnez vous-même une suite de noeuds de l'arbre binaire. La cohérence de cette suite sera vérifiée au moment de la transformée inverse. |
|
Meilleur_Niveau/t/rang/i |
Algorithme Best Level : Sélection automatique du niveau de décomposition de plus faible coût. La fonction de coût à utiliser est communiquée au module. |
|
Meilleure_Base/t/rang/i |
Algorithme Best Basis : Sélection automatique de la suite de noeuds de plus faible coût. La fonction de coût à utiliser est communiquée au module. |
En sortie de ces modules sont communiqués deux vecteurs :
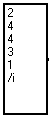
Car les noeuds sélectionnés sont : un noeud niveau 2, puis deux noeuds niveau 4, puis un noeud niveau 3 et enfin un noeud niveau 1.
Ce vecteur est utilisé lors de la Transformée en Paquets d'Ondelettes Inverse pour reconstruire le signal à partir des coefficients aux différents niveaux. Vous n'avez à le spécifiez vous-même explicitement que si vous utilisez le module manuel
4.4.3. Transformée en Paquets d'Ondelettes Inverse
Le module
IWPT1D/t/r/i reconstruit le signal de longueur N à partir des N coefficients de Paquets d'Ondelettes sélectionnés (vecteur selon la variable /t) et de la suite des niveaux des noeuds sélectionnés (vecteur selon la variable /i). Les paramètres de cette transformée inverse (méthode de traitement des effets de bords et offset du filtre) sont réglables en double-cliquant à l'intérieur du module, et sont disponibles en faisceau sur la borne inférieure.Le nombre d'itérations à effectuer est guidé par le choix des noeuds de l'arbre binaire. Par conséquent, la première borne du faisceau de sortie n'a pas de signification dans ce contexte.
Il est possible de former ce faisceau de paramètres à l'aide de la souris en utilisant le module élémentaire
Parametres_wpkt. Il s'agit du même module que pour la transformée directe, mais le nombre d'itérations défini n'est pas utilisé, puisque c'est le choix des noeuds de l'arbre binaire qui contrôle les itérations de la transformée inverse.Enfin, pour réaliser une transformée en paquets d'ondelettes inverse en communiquant directement le faisceau de paramètres, utilisez le module élémentaire
IFWPT_1D/t/r/rang.
4.4.4. Débruitage par décomposition en Paquets d'Ondelettes
Le principe est similaire au débruitage par décomposition en ondelettes :
Pour ne seuiller que les coefficients de détails, il est nécessaire de les séparer auparavant de l'ensemble des coefficients de paquets d'ondelettes. Pour cela, utilisez la macro élementaire
Isole_details_wpkt/t/i à la suite du module de sélection des noeuds. Après le seuillage, reconstruisez le vecteur de coefficients complet (Approximation + détails seuillés) à l'aide du module élémentaire Colle_D_A_wpkt/t. Enfin, procédez à une transformée inverse avec les mêmes paramètres que la transformée directe : utilisez le module IFWPT_1D dans ce but.
Exemple
Le programme MUSTIG ci-dessous procède au débruitage d'un signal par décomposition en paquets d'ondelettes selon l'algorithme "Meilleure Base", seuillage des coefficients et reconstruction du signal.
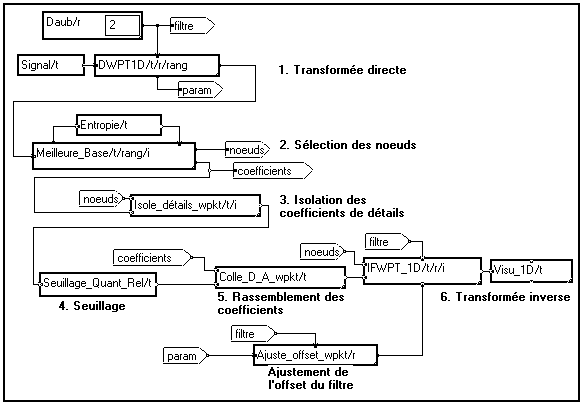
Une macro intégrée de débruitage par décomposition en Paquets d'Ondelettes, seuillage, puis reconstruction est disponible dans la boîte "Utilitaires" de la bibliothèque. Tous les paramètres de calcul sont réglables à l'aide de la souris. Le signal débruité est disponible en sortie du module.
Personnalisation des modules intégrés
Vous pouvez bien sûr déverrouiller le module après l'avoir placé dans votre fenêtre de programmation (Alt+W), et créer une autre borne de sortie (Maj+Clic) afin d'y acheminer à d'autres éléments du calcul : coefficients de paquets d'ondelettes bruts ou seuillés, etc., afin de développer vos propres applications.
ANNEXE 1 : Liste des modules de la bibliothèque ONDELETTES pour MUSTIG
Le tableau ci-dessous contient la liste des modules proposés dans la bibliothèque Ondelettes pour MUSTIG 4.5., avec un bref descriptif de leur fonction. Consultez sous MUSTIG l'aide en ligne de chaque module (ALT+H) pour connaître les branchements et les détails de fonctionnement.
|
Ondelettes de Base |
||
|
Ondelettes continues pour la Transformée Continue |
||
|
Mexican_Hat/t |
Génère l'ondelette "Chapeau Mexicain" à partir d'un support temporel selon la variable /t |
|
|
Morlet_Re/t |
Génère la partie réelle de l'ondelette de Morlet à partir d'un support temporel selon la variable /t |
|
|
Morlet_Im/t |
Génère la partie imaginaire de l'ondelette de Morlet à partir d'un support temporel selon la variable /t |
|
|
8th_Gauss/t |
Génère l'ondelette "Dérivée huitième de la Gaussienne" à partir d'un support temporel selon la variable /t |
|
|
Filtres passe-bas pour l'analyse multirésolution |
||
|
Haar/r |
Filtre passe-bas de Haar selon la variable /r |
|
|
Daub/r |
Filtre passe-bas de Daubechies selon la variable /r |
|
|
Symlets/t |
Filtre passe-bas Symlets selon la variable /r |
|
|
Lemarie4/t |
Filtre passe-bas de Battle-Lemarie selon la variable /r |
|
|
Choix_Ondelettes/r |
Choix entre les quatre filtres ci-dessus à l'aide de la souris |
|
|
Filtre->PSI/t/r |
Calcul de l'ondelette associée à un filtre pour une échelle donnée (spécifiée en double-cliquant sur le module) |
|
|
Filtre->PSI_2D/x/y/r |
Calcul de l'ondelette à deux dimensions associée à un filtre pour une échelle donnée (spécifiée en double-cliquant sur le module) |
|
|
Transformées |
||
|
Transformée Continue |
||
|
CWT/t/m/n |
Transformée Continue en Ondelettes d'un signal de la variable /t. Production des coefficients selon les variables /m et /n |
|
|
Synthèse/m/n/t |
Synthèse d'un signal à partir des coeffcients |
|
|
Analyse Temps Echelle/t |
Module complet d'analyse temps-echelle d'un signal avec visualisation en vraie résolution temps-fréquence. |
|
|
Modules Elementaires |
||
|
RpeZ/m |
Génération d'une rampe d'entiers relatifs selon la variable /m |
|
|
a0_b0->am_bn/m/n |
Génération d'un vecteur de facteurs d'echelle selon /m et d'une matrice de décalage selon /m et /n à partir des pas a0 et b0. |
|
|
Wcoef/t |
Calcul du produit scalaire entre un signal et une ondelette |
|
|
dt0_k0_s0/m/n/t |
A partir d'une collection d'ondelettes incidente selon /t, /m et /n, calcul de la résolution temporelle, de la position fréquentielle et de la résolution fréquentielle de l'ondelette de base. |
|
|
Position_temps/t |
Position et résolution (étendue) d'une ondelette |
|
|
Position_frequence/t/f |
Position fréquentielle et étendue spectrale d'une ondelette (par calcul de sa Transformée de Fourier) |
|
|
Facteur_de_Norm/m/n/t |
Calcul du facteur de normalisation à utiliser lors de la Transformée Continue Inverse |
|
|
Transformée en Ondelettes Discrète |
||
|
FWT/t/x/i |
Transformée Rapide Discrète en Ondelettes (directe ou inverse) d'un signal selon /t, avec un filtre selon /x, détails produits selon /t et /i. |
|
|
FWT_2D/x/y/r |
Transformée Rapide Discrète en Ondelettes (directe ou inverse) d'une image selon /x et /y, avec un filtre selon /r. |
|
|
Modules Elémentaires |
||
|
DWT1D/t/r |
Transformée en Ondelettes discrète directe ou inverse avec passage des paramètres par faisceau externe |
|
|
DWT2D/x/y/r |
Transformée 2D en Ondelettes discrète directe ou inverse avec passage des paramètres par faisceau externe |
|
|
Parametres/t/r |
Production d'un faisceau de paramètres pour les transformées en ondelettes 1D ou 2D discrètes à l'aide de clics souris. |
|
|
Change_sens |
Inverse le sens de la transformée dans le faisceau de paramètres |
|
|
Ajuste_offset/r |
Corrige l'offset du filtre centré en fonction de sa longueur de façon à assurer une bonne reconstruction du signal |
|
|
Transformée en Paquets d'Ondelettes |
||
|
DWPT1D/t/r/rang |
Transformée Rapide Directe en Paquets d'Ondelettes d'un signal selon /t, avec un filtre selon /r, le niveau de décomposition est paramétré par /rang. |
|
|
IWPT1D/t/r/i |
Synthèse d'un signal selon /t à partir des coefficients de Paquets d'Ondelettes sélectionnés dans l'arbre binaire de décomposition |
|
|
Sélection des Niveaux |
||
|
Niveau_Constant/rang/i |
Sélection des noeuds d'un niveau de décomposition dans l'arbre binaire de décomposition en Paquets d'Ondelettes |
|
|
Combinaison_de_Noeuds/t/rang/i |
Sélection d'une combinaison quelconque de noeuds dans l'arbre binaire de décomposition en Paquets d'Ondelettes |
|
|
Meilleur_Niveau/t/rang/i |
Sélection du niveau de plus faible cout dans l'arbre binaire de décomposition en Paquets d'Ondelettes |
|
|
Meilleure_Base/t/rang/i |
Sélection de la combinaison de noeuds de plus faible cout dans l'arbre binaire de décomposition en Paquets d'Ondelettes |
|
|
Entropie/t |
Calcul de l'entropie de Shannon d'un signal |
|
|
Entropie_non_norm/t |
Calcul de l'entropie non normalisée d'un signal |
|
|
Log_Energie/t |
Calcul du "Log Energie" d'un signal |
|
|
Dimension/t |
Calcul de la dimension d'un signal |
|
|
Compression/t |
Calcul de la compression d'un signal |
|
|
Energie=1/t |
Normalisation d'un signal |
|
|
Norme/t |
Calcul de la Norme Lp d'un signal |
|
|
Prop_Sup/t |
Calcul de la proportion d'échantillons supérieurs en valeur absolue à un seuil |
|
|
Prop_Sup_Rel/t |
Calcul de la proportion d'échantillons supérieurs en valeur absolue à un seuil défini en fonction du Max du signal. |
|
|
Choix fonction de cout/t |
Choix d'une fonction de coût à l'aide d'une interface souris. |
|
|
Modules Elémentaires |
||
|
DFWPT_1D/t/r/rang |
Transformée en paquets d'ondelettes directe avec passage des paramètres par faisceau externe |
|
|
IFWPT_1D/t/r/i |
Transformée en paquets d'ondelettes inverse avec passage des paramètres par faisceau externe |
|
|
Parametres_wpkt/t/r |
Production du faisceau de paramètres pour les transformées en paquets d'ondelettes à l'aide de clics souris. |
|
|
Ajuste_offset_wpkt/r |
Corrige l'offset du filtre en fonction de sa longueur de manière à assurer une bonne reconstruction. |
|
|
Sépare_paquets/t/i/rang |
Séparation des coefficients de Paquets d'Ondelettes par niveau (/rang) et par noeud (/i). La longueur de la variable /i dépend de la variable /rang. |
|
|
Separe_pkts_nondyna/t/i/rang |
Idem, mais la longueur de la variable /i est fixe, égale à sa valeur maximum. Les coefficients des niveaux inférieurs sont complétés avec des zéros. |
|
|
Signaux Test |
||
|
Signaux 1D |
||
|
FM+Bruit/t |
Génération d'une modulation linéaire de fréquence bruitée selon la variable /t. |
|
|
Signaux 2D |
||
|
Dirac2D/x/y |
Génération d'un Dirac dans une matrice nulle |
|
|
Carre/x/y |
Génération d'un carré centré plein dans une image |
|
|
Carre-diag/x/y |
Génération d'un carré vide avec ses diagonales |
|
|
Algorithmes de Séparation des coefficients et de Seuillage |
||
|
Manipulation des coefficients sur signaux 1D |
||
|
Recolle_Di/i/t |
Concaténation des coefficients d'ondelettes (en vue d'un seuillage par exemple) |
|
|
Sépare_Di/i/t |
Opération inverse : séparation des coefficients concaténés (par exemple après seuillage) |
|
|
Regroupe_D_A/i/t |
Regroupe les coefficients de détails et les coefficients de moyenne en un vecteur près à subir une Transformée en Ondelettes Discrète Inverse. |
|
|
Reconstruit_Di/t/i/x |
Conduit une série de Transformée en Ondelettes Discrète Inverses afin de reconstruire des signaux de détails de longeur N à partir de chaque niveau de décomposition. |
|
|
Reconstruit_A/t/x |
Reconstruit le signal de moyenne de longueur N à partir des coefficients du dernier niveau de décomposition. |
|
|
Manipulation des coefficients sur signaux 2D |
||
|
Matrice_A/x/y |
Séparation de la matrice de Moyenne (Average) de la matrice de coefficients d'ondelettes 2D |
|
|
Vectorise_Dij/x/y |
Concaténation des détails d'une image transformée en vue par exemple d'un seuillage |
|
|
Matrice_Dij/x/y |
Opération inverse : reconstruction des détails concaténés (éventuellement après seuillage). |
|
|
DhDvDd/x/y |
Séparation des détails horizontaux, verticaux et diagonaux (par exemple pour un traitement séparé) |
|
|
DhDvDd->Dij/x/y |
Opération inverse : reconstruction de la matrice de détails à partir des matrices de détails horizontaux, verticaux et diagonaux. |
|
|
Assemble_A_D/x/y |
Assemblage de la matrice de Moyenne et de la matrice de Détails en une matrice prête à subir une Transformée en Ondelettes Discrète 2D Inverse. |
|
|
Algorithmes de Seuillage des coefficients |
||
|
Seuillage Absolu |
Les coefficients inférieurs en valeur absolue à un seuil fixe sont mis à zéro. |
|
|
Seuillage Relatif/t |
Idem mais le seuil est calculé comme un certain pourcentage du maximum de la valeur absolue du signal |
|
|
Shrinkage Absolu |
Opération de rétrécissement des coefficients avec un seuil fixe |
|
|
Shrinkage Relatif /t |
Idem mais le seuil est calculé comme un certain pourcentage du maximum de la valeur absolue du signal |
|
|
Donoho Shrinkage/t |
Rétrécissement avec calcul du seuil selon Donoho |
|
|
Seuillage_Quantitaif_Abs/t |
Seuillage par conservation d'un nombre fini de coefficients (les plus grands), ce nombre étant ajustable en double-cliquant sur le module |
|
|
Seuillage_Quantitaif_Rel/t |
Seuillage par conservation d'un nombre fini de coefficients (les plus grands), ce nombre étant calculé comme un pourcentage du nombre total de coefficients |
|
|
Choix_Seuillage/t |
Macro intégrée permettant de choisir parmi les méthodes ci-dessus à l'aide de la souris |
|
|
% non nuls/t |
Calcul du pourcentage d'échantillons non nuls dans un signal (pour évaluer l'efficacité d'un seuillage) |
|
|
Visus Spécifiques et Utilitaires |
||
|
Visu_PTE/t/m/n |
Utilisé après une décomposition par Transformée Continue en Ondelettes. Permet de représenter le contenu temps-échelle du signal en tenant compte de la résolution temps-fréquence de l'ondelette choisie. |
|
|
Visu_2D_BM/x/y |
Visualisation d'une image sous la forme d'une BitMap |
|
|
DEBRUITAGE/t |
Débruitage d'un signal 1D par décomposition en ondelettes. Tous les paramètres sont réglables à l'aide de la souris en double-cliquant sur le module. |
|
|
DEBRUITAGE_WPKT/t |
Débruitage d'un signal 1D par décomposition en paquets d'ondelettes. Tous les paramètres sont réglables à l'aide de la souris en double-cliquant sur le module. |
|
|
DEBRUITAGE_2D/x/y |
Débruitage d'un signal 2D (image, matrice) par décomposition en ondelettes. Tous les paramètres sont réglables à l'aide de la souris en double-cliquant sur le module. |
|
ANNEXE 2 : Liste des exemples fournis
INDEX de la bibliothèque Ondelettes pour MUSTIG
Aidez-nous à améliorer cette bibliothèque et à la faire évoluer dans le sens de vos besoins. Si vous constatez un défaut de fonctionnement, ou bien si vous souhaitez voir figurer certaines fonctionnalités dans les prochaines versions de cette bibliothèque, photocopiez le bordereau ci-dessous et faites le parvenir par courrier ou télécopie à :
Nom : Prénom : Fonction :
Société / Laboratoire :
Matériel : PC MAC UNIX Processeur : Syst. Exploitation :
Remarques / Défauts constatés sur la bibliothèque Ondelettes :
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Je voudrais voir figurer dans les prochaines versions de la bibliothèque Ondelettes pour MUSTIG les fonctionnalités suivantes :
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________