LE LANGAGE GRAPHIQUE
Table des matières
Si vous souhaitez améliorer immédiatement votre savoir pratique du système d'exploitation MUSTIG, référez-vous au tutoriel : vous serez capable de comprendre, à travers un exemple, à la fois le processus de calcul et l'éditeur graphique.
2-1 Variables
2-2 Macros
2-3 Le graphe de la dépendance : le graphe de base
2-4 Compacter le graphe en paquets
2-5 Mode fonctionnel
2-5-1 Répétition implicite
2-5-2 Epandage automatique
2. LE LANGAGE GRAPHIQUE
Le langage utilisé par MUSTIG peut être décrit de points de vue différents. La forme de base est celle d'un diagramme de dépendance complété par une syntaxe qui autorise une description de seulement un motif d'un diagramme périodique en créant des paquets, et de règles qui autorisent à condenser la représentation. Les sous-ensembles du graphe peuvent être compactés en " macros ". Dès qu'un nombre suffisant de macros est présent (celles de la bibliothèque standard par exemple) il est possible de quitter la forme de base et de passer à une forme utilitaire beaucoup plus proche d'une description mathématique. La définition de la macro " Retard " (z-1) permet la description des structures de filtres dans une forme du diagramme de flux. Finalement, une analyse dans une forme séquentielle, plus classique, est toujours possible et peut être utilisée surtout pour les applications temps-réel.
Tous ces formes sont des approches différentes du langage. Le code de calcul produit par le compilateur, en commençant d'une forme ou de l'autre sera souvent le même. Les formes différentes peuvent être mélangées dans une analyse unique.
Une analyse est créée par un graphe qui définit les rapports entre signaux. Ces signaux sont fonctions d'une ou plusieurs variables discrètes.
Exemples :
f(t) signal temporel, fonction de la variable temporelle " t "
f(x,y) signal spatial, fonction de deux variables d'espace " x " et " y "
f(x,y,t) signal spatio - temporel, fonction de variables temps et espace.
C'est très important de distinguer cette notion de variable comme un support du signal de celle utilisée dans les langages de programmation procéduraux où la référence est faite à une cellule de mémoire dont le contenu peut être changé. Ici la notion se rapproche de la " fonction d'une variable " utilisée dans le vocabulaire mathématique.
Ces variables (discrètes) reçoivent un nom et leurs caractéristiques sont comme suit :
Toutes ces variables ont un nombre fini de valeurs (excepté une : le temps, dans les applications d'analyse en temps-réel). La définition de ces variables est attachée au signal. Pour les techniques de définition des variables, voir la section 4-3
Une macro est un sous-ensemble du graphe rendu compact représenté par une boîte et pourrait être aussi petite que les boîtes des modules de base ou très grande, contenant des éléments de base aussi bien que d'autres macros. Elle est identifiée par un nom. Ce nom peut être suivi, séparés par un " / " , par le(les) nom(s) des variables utilisées par la macro :

Dans l'exemple ci-dessus, l'opérateur macro créé est nommé " Ma macro ". La chaîne " /t/f/x " entrée après le nom indique que cette macro traite trois variables nommées t, f et x.
Si le nom des variables est modifié, l'éditeur modifie tous les noms correspondants à l'intérieur de la macro. Donc si une macro opère sur une variable nommé x par exemple, et vous voulez maintenant qu'elle traite un signal porté par une variable nommée y, vous devez juste changer le nom par Maj+ctrl+clic sur le nom des variables sur le devant de la macro.
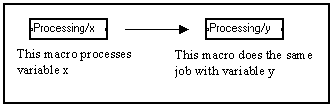
En fait, les macros sont utilisées pour réduire la dimension du graphe sur l'écran commodément et le rendre plus lisible. Ils ne changent rien dans le processus du compilateur, car les mêmes calculs sont faits par le compilateur.
Utiliser des macros permet la description du système et sous-système aussi bien que la réduction de l'espace pris par les fichiers de sauvegarde des graphes puisque que les macros sont sauvegardés seulement une fois, ou pas du tout si elles viennent de la bibliothèque de base.
2-3 Le graphe de dépendance : le graphe de base
L'analyse est décrite sous la forme d'un graphe qui définit les relations de dependance (arithmétique, logique...) entre les valeurs (scalaire ou vecteur) ; ce graphe ne prend pas en considération la chronologie du processus de génération. Toutes les mémoires ne paraissent pas. Ce graphe du dependance ne doit pas inclure de boucles.
Il est saisi directement dans sa forme graphique et est fait d'opérateurs mathématiques élémentaires (voir la figure ci-dessous par exemple). Ces opérateurs sont tracés comme des rectangles, avec des " bornes " où des " fils " de valeurs se propageant sont " connectés ". Les opérateurs sont identifiés par un nom ou un symbole dans le rectangle.
Quelques opérateurs opèrent sur des scalaires, d'autres sur des vecteurs, dans ce dernier cas, la(les) variable(s) doivent être entrées après le nom séparées par le signe " / " (slash) .
2-4 Compacter le graphe en paquets
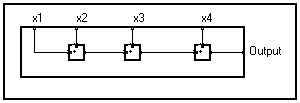
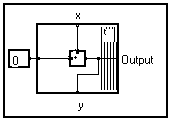
Dans beaucoup d'applications, quelques entrées et sorties du diagramme sont des vecteurs et le diagramme a des structures répétées qui sont représentées dans un langage mathématique par des équations récursives. Le graphe peut être représenté comme un paquet d'une manière compacte. Seulement un motif est sorti de la structure périodique du graphe, et placé dans un rectangle avec un bord plus épais dans la direction où le modèle doit être répété pour obtenir le graphe entier (voir la figure ci-dessous).
Par convention, le bord le plus épais est placé dans la direction d'indices croissant. La ligne plus épaisse représente d'une manière schématique l'épaisseur du paquet. L'ensemble compacté sera appelé un paquet (si nous pensons comment il a été créé) ou une " boucle " si nous pensons à son équivalent dans les langages de programmation classiques.
Pour obtenir une meilleur compréhension de cette notion, imaginez que tous les motifs identiques du graphe ont été dessinés sur des rectangles du carton, puis que tout a été rassemblé en un paquet, comme des cartes à jouer.
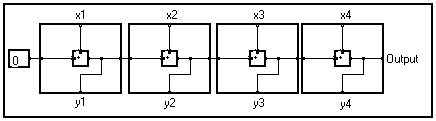
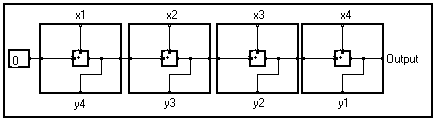
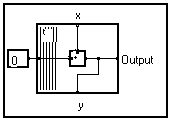
Une borne placée sur le bord plus épais a nécessairement une borne correspondante sur le bord qui lui fait face. Une sortie correspond toujours à une entrée et réciproquement. C'est une conséquence immédiate de la façon dont le paquet est constitué : quand les motifs étaient côte à côte, une sortie était directement reliée à une entrée du motif adjacent. Ces bornes sont appelées " bornes frontales ".
Sur les deux autres côtés, on peut trouver (ou non) des bornes qui sont appelées " bornes latérales ". La laiison sur à une borne latérale correspond à la représentation unique de l'ensemble des liaisons de chaque motif originel. Supposons que toutes les liaisons du graphe initial étaient des valeurs scalaires ; alors l'ensemble des scalaire forme un vecteur. Pour être plus précis, nous écrirons que c'est une fonction de la variable utilisée comme un index dans les motifs et indiquée dans le bord plus épais du paquet.
Note : Comme le bord du paquet est tracé dans un tarit plus épais, ce serait logique de faire le même pour tracer les liaisons latérales, cela montrerait leur caractéristique vectorielle, mais cela rendrait le graphe trop lourd.
Compacter en paquets peut être répété si le diagramme initial présente une fréquence double. Maintenant, les valeurs des entrées frontales ne sont plus scalaires : les sorties latérales deviennent fonctions des mêmes variables que les entrées frontales plus la variable du paquet .
La même chose pourrait être appliquée aux entrées latérales, mais le mécanisme d'épandage permet au signal de ne pas être fonction de la variable du paquet .
La disposition du graphe est rendue plus facile en utilisant les modes suivants de fonctions vectorielles, deux propriétés simplificatrices de MUSTIG.
Si un signal vectoriel est appliqué à un opérateur scalaire, tous les éléments du vecteur sont affectés par l'opération. Plus généralement, si un signal dépend de plus de variables que l'opérateur ne connait, l'opération est effectuée sur chaque élément selon la(les) variable(s) supplémentaire(s).

Si un vecteur et un scalaire sont appliqués à un opérateur scalaire, l'opération est efectuée sur chaque élément du vecteur avec la même valeur scalaire. Par exemple, si l'opérateur de l'addition est appliqué à un scalaire et un vecteur, le scalaire sera ajouté à chaque élément du vecteur : la sortie est par conséquent un vecteur.
Plus généralement, si deux signaux sont appliqués à un opérateur avec l'un d'eux selon une variable de moins que l'autre, l'opérateur devient une fonction de cette variable, mais sa valeur est une constante le long de cette variable.
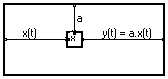
Dans le cas d'un opérateur vectoriel, les signaux doivent être une fonction des variables attendues par l'opérateur.
La répétition implicite réduit le graphe en enlevant des opérateurs des paquets. Donc, les bords latéraux des paquets sont des limites perméables : les opérateurs peuvent les traverser; quand la continuité des connections est maintenue, rien n'est changé dans la signification du graphe.
|
<=> |
|
Cette règle autorise à appliquer à un signal multidimensionnel toute analyse prévue pour des signaux d'une seule sdimension. Ces deux règles, combinées avec la possibilité de compacter des parties du graphe en macros qui agissent comme de nouveaux opérateurs, permet à beaucoup de problèmes d'analyse d'être entièrement décrits dans la forme d'un diagramme fonctionnel, sans appeler la forme de base du diagramme de dépendance.
Les systèmes d'analyse tels que des filtres sont souvent décrits par les diagrammes de flux. Ce diagramme est une transcription directe des équations de différence du filtre, en utilisant des opérateurs arithmétiques et des retards élémentaires.
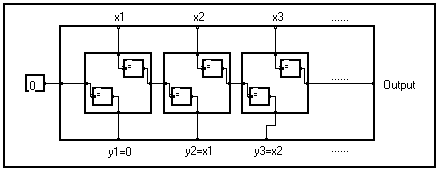
Ces retards, dont la fonction de transfert en z est " z-1 " peuvent être facilement construits à travers la syntaxe de base . On doit seulement tracer le diagramme de dépendance qui lie les échantillons d'entrée aux échantillons de sortie du retard. Ce diagramme n'a aucun opérateur, il a des liaisons seulement. La forme compactée en paquets est déduite et la forme de macro est réalisée pour obtenir l'opérateur du Retard.
S'il vous plaît notez qu'il est possible d'appliquer cet opérateur à un signal selon plusieurs variables, le retard est exécuté selon la variable indiquée dans le paquet et trouvée sur la macro.
En fait l'éditeur graphique empêche de construire un paquet sans opérateur, donc les opérateurs inefficaces " = " sont introduits.
![]()
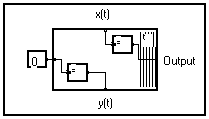
Le premier échantillon du signal différé ne dépend pas du signal de l'entrée. Sa valeur, donnée par l'entrée frontale du paquet, est mise à 0 dans la macro de la bibliothèque standard mais elle peut être changée.
En raisonnant en système de simulation temporelle discrète, cette première valeur correspond à l'état initial de la cellule mémoire. Si besoin est, cette valeur peut être accédée à travers une entrée supplémentaire de la macro. De la même façon, la dernière valeur de l'entrée peut être sortie, autrement elle est normalement perdue. Une cellule généralisée est obtenue avec quatre bornes comme montré ci-dessus.
Un diagramme de fluxt peut avoir des boucles. Cela peut paraître contradictoire avec le fait que les boucles ne sont pas autorisées dans le graphe de dépendance. En fait, quand on remplace les macros " z-1 " par leur contenu, un graphe sans boucles est obtenu et le calcul est possible.
L'intégrale indéfinie y(t) d'un signal x(t) de la variable discrète t peut être calculé à travers la relation de récurrence :
y(t) = x(t)+y(t-1) avec y(0) = x(0) pour t = 0
Cette relation peut être exprimée par le diagramme de flux montré ci-dessous :
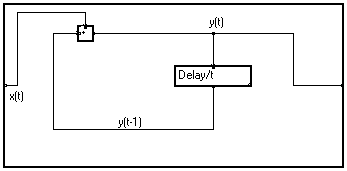
En expansant la macro Retard/t, nous obtenons :
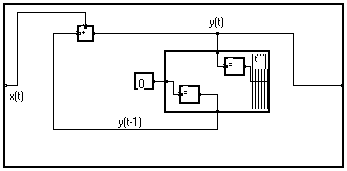
Nous avons vu que les limites latérales d'un paquet peuvent être traversées sans changer la signification du graphe. Donc l'additionneur peut être entré dans le paquet :
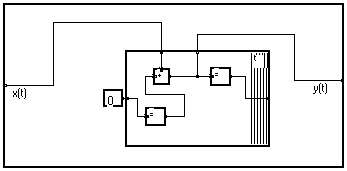
Le graphe peut être encore simplifié, en donnant le même diagramme que celui obtenu en commençant par le diagramme de dépendance :
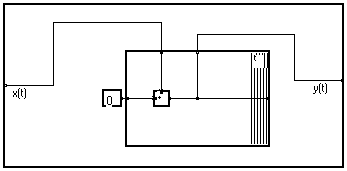
Pratiquement, la forme compacte dans la macro " Somme/t " sera beaucoup plus facile à lire :
![]()