Interpolation
Contenu
Augmentation du nombre de points d'un signal.
Mots clés
interpolation, suréchantillonnage, filtrage, multicadence
Fichiers MUSTIG associés
Exemples commentés voisins
Principes théoriques
L'augmentation du nombre de point d'un signal revient à augmenter la fréquence d'échantillonnage du signal continu dont il est issu (ou dont il pourrait être issu). Cette opération revient à calculer de nouveaux échantillons sur ce signal continu et donc de réaliser une interpolation. Cette interpolation peut s'approximer par des interpolations linéaires ou polynomiale à partir des échantillons voisins de celui qui est recherché (cf exemples.....). Sa réalisation rigoureuse consiste en un filtrage de type passe-bas. Il s'agit alors d'un filtre qui modifie la fréquence d'échantillonnage (filtrage "multi-cadence"). Une façon rapide de réaliser cette opération est d'utiliser la Transformée de Fourier Discrète (TFD). Voir l'exemple "interpolation par TFD".
Réalisation MUSTIG
On peut considérer l'opération d'augmentation de la fréquence d'échantillonnage (par un facteur entier) comme le remplacement de chacun des points du signal par un ensemble de points qui peut lui-même être considéré comme un signal. L'ensemble de ces signaux intermédiaires peut être vu comme une fonction à deux dimensions. L'opération d'augmentation de la fréquence d'échantillonnage se décompose ainsi en deux phases : création de l'ensemble des signaux intermédiaires, puis mise bout à bout de ces signaux par le module "recolle".
Insertion de "0"
(L'augmentation de la fréquence d'échantillonnage par ajout de "0" sera nécessairement suivie d'un filtrage passe-bas. Il sera plus efficace d'utiliser un filtre multicadence).
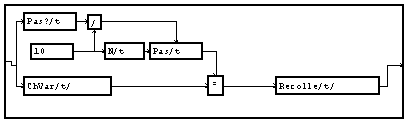
Les signaux intermédiaires sont constitués d'une première valeur égale à celle du signal, puis de valeurs nulles. On pourrait utiliser un générateur d'impulsion de Dirac multiplié par celle valeur. La graphe suivant est plus simple.
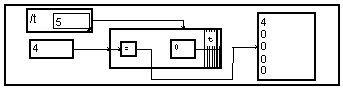
Notons que le module "=" est ineffectif, mais que sa présence est imposé par l'éditeur graphique de MUSTIG.
On peut voir que le premier échantillon de la sortie latérale (en bas) du paquet indicé par "t" est l'entrée frontale (à gauche), alors que toutes les autres proviennent de la constante nulle. Ce paquet forme une fonction de "t" à partir d'un scalaire. Si on applique à son entrée frontale un signal fonction d'une autre variable "b", on obtiendra un ensemble, indicé par "b", de fonctions de "t", donc une fonction de "t" et "b". Le module "recolle" permet de mettre bout à bout ces fonction pour ne plus former qu'une fonction de la seule variable "t". Pour pouvoir appliquer cet graphe à un signal fonction de la variable "t", il est nécessaire de transformer provisoirement "t" en "b" par le module "ChVar".
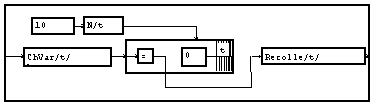
Nous obtenons une première réalisation de la macro de suréchantillonnage par ajout de "0". Il convient de la compléter pour prendre en compte le pas d'échantillonnage du signal d'entrée.
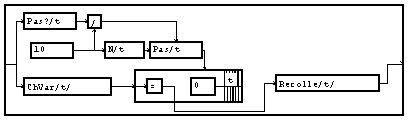
Interpolation d'ordre "0"
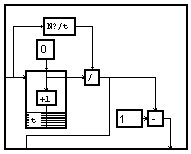
L'interpolation d'ordre "0" revient à répéter chaque échantillon. On peut utiliser une structure tout à fait analogue à la structure précédente.
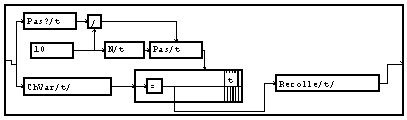
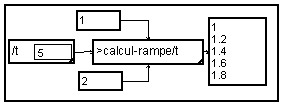
La fonction de répétition de valeurs identiques peut
simplement être faite en ajoutant la nouvelle variable "b" par le
module![]() . Nous obtenons alors la macro "Suréchantillonne_1"
. Nous obtenons alors la macro "Suréchantillonne_1"
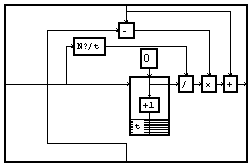
Interpolation d'ordre "1"
L'interpolation d'ordre 1, ou interpolation linéaire, revient à insérer des point alignés, c'est à dire une rampe entre deux points. On peut pour cela partir de la macro "Rampe" de la bibliothèque. Nous proposons une variante légèrement plus efficace.
Ce générateur de rampe est utilisé entre l'échantillon courant et son précédent. Ce dernier est obtenu par un retard.
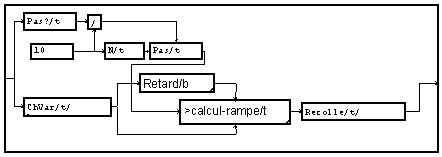
Interpolation par filtrage
L'interpolation linéaire peut déjà être considérée comme un filtrage simplifié de type RIF (réponse impulsionelle finie) à deux coefficients. Pour mieux le faire apparaître on peut mettre le graphe sous la forme ci-dessous.
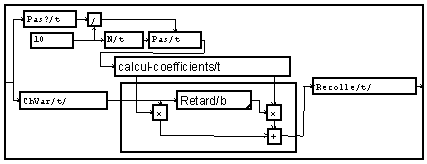
Le calcul des coefficients étant fait par :
Nous obtenons une forme de filtre multicadence généralisable.
Remarque
Toutes les structures précédentes ne conviennent que pour des signaux courts. Pour des signaux longs, ou pour un fonctionnement temps réel, il est indispensable de se passer des opérateurs "ChVar" et "recolle", qui nécessitent tous deux d'avoir le signal entièrement en mémoire.