Interpolation par TFD
Contenu
Augmentation du nombre de point d'un signal en utilisant la Transformée de Fourier Discrète pour réaliser le filtrage
Mots clés
interpolation, suréchantillonnage,TFD
Fichiers MUSTIG associés
Exemples commentés voisins
Utilisation de la TFD. Interpolation, filtrage par blocs.
Principes théoriques
Interpolation d'un signal temporel
L'augmentation du nombre de point d'un signal revient à augmenter la fréquence d'échantillonnage du signal continu dont il est issu (ou dont il pourrait être issu). Cette opération revient à calculer de nouveaux échantillons sur ce signal continu et donc de réaliser une interpolation. Cette interpolation peut s'approximer par des interpolations linéaires ou polynomiale à partir des échantillons voisins de celui qui est recherché (cf exemples.....). Sa réalisation rigoureuse consiste en un filtrage de type passe-bas. Une façon rapide de réaliser cette opération est d'utiliser la Transformée de Fourier Discrète (TFD).
Soit un signal continu à durée limité et spectre limité (approximativement bien sur...). Son échantillonnage à la fréquence fe donne un signal discret de N points. La TDF de ces N points donne une transformée de N points que l'on peut séparer en N/2 points de fréquence négatives et N/2 points de fréquences positives. Le transformée du même signal continu échantillonné avec une fréquence fe' = fe.M/N possède M points (M>N). La transformée de ces M points donnera M points dont N seront identiques aux point précédent et les autres seront nuls, puisque le signal est alors échantillonné à une fréquence supérieurs à la fréquence de Shannon.
Augmenter la fréquence d'échantillonnage temporelle revient donc à ajouter des points nuls en haute fréquence sur la TFD. Ces hautes fréquences sont situées autour du point N/2. Il faut donc "écarter" les deux moitiés de la TFD et insérer de "0". Dans le cas d'un signal réel, puisqu'on ne garde qu'une moitié, il suffit d'ajouter des "0" après celle-ci.
Cette technique ne permet que des multiplications de fréquence par des nombres rationnels (quotients de deux entiers). Si on utilise un algorithme de TFD rapide restreint à des tailles de signaux puissance de deux, on ne peut alors que multiplier la fréquence par une puissance de deux.
Interpolation d'un signal fréquentiel
De façon analogue, pour interpoler un signal dans le domaine des fréquences, il faut ajouter des points nuls au signal temporel. Mais il faudra les ajouter en fin du signal.
Réalisation MUSTIG
Signal réel
L'augmentation du nombre de point en fréquence se fait simplement par le module "partie".

La nouvelle longueur est contrainte à une puissance de 2 moins 1.
On peut réaliser une macro plus générale qui augmente le nombre de point d'un facteur défini (puissance de 2).
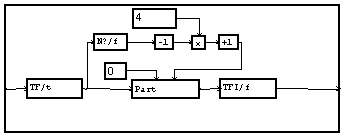
Le module "N?/f" récupère le nombre de point initial. Sachant que MUSTIG ne garde que N/2+1 point de la TFD d'un signal réel, on enlève 1 pour obtenir N/2 avant de multiplier.
Signal complexe
Pour insérer des "0" au milieu de la TFD on effectue un décalage circulaire de N/2. Un décalage inverse est effectué après l'ajout de "0" par le module "Partie"
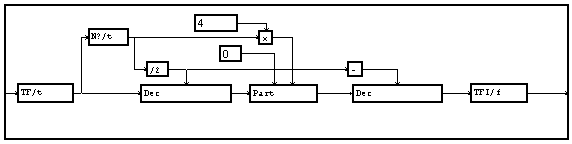
On faisant fonctionner les exemples, on remarquera que les graduations le long de l'axe du temps sont identiques avant et après interpolation : MUSTIG gère les changements de fréquence d'échantillonnage, c'est donc le temps, en seconde, qui est indiqué, et non pas les numéros des points.
Réduction de la fréquence d'échantillonnage
Les structures précédentes peuvent également fonctionner en réduction de fréquence. Dans ce cas le module "Part" supprime des points en haute fréquence, ce qui revient à multiplier par une porte. Cela réalise un filtrage non optimal. Pour améliorer la qualité du filtre, il faudra ajouter à la suite de ce module "Part" une multiplication par les coefficients souhaités.
Interpolation par blocs de signaux longs
Un signal long devra être divisé en plusieurs blocs. L'opération d'augmentation de la fréquence d'échantillonnage contenant implicitement un filtrage, il faut utiliser une structure semblable à celle du filtrage par blocs (voir exemples "f_morcea.MTG", décrit dans "convolution par TFD") pour supprimer la circularité de la TFD. On effectue l'opération sur des blocs de taille double, et on ne garde que la bonne moitié de chaque résultat.
Interpolation d'un spectre
L'interpolation du signal dans le domaine spectrale peut se faire de façon duale, en ajoutant des valeurs nulles dans le domaine temporel. Il suffit donc de faire une transformée de Fourier inverse, allonger le signal à l'aide du module "Part", et refaire une transformée de Fourier directe. Ce besoin existe généralement en analyse spectrale, il suffira donc de faire une seule transformée de Fourier directe après avoir allongé le signal. (Voir exemple "Apodisation")