Apodisation
Contenu
Techniques d'apodisation : réduction des lobes secondaires en analyse spectrale. (en synthèse de filtre)
Mots clés
apodisation
Fichiers MUSTIG associés
Exemples commentés voisins
Utilisation de la TFD, Interpolation
Principes théoriques
Pour effectuer l'analyse spectrale d'un signal à durée non limitée, on calcule la transformée de Fourier d'une portion seulement de ce signal. On peut modéliser cette opération par la multiplication du signal par un signal "porte" de durée égale à la durée d'analyse. Cela se traduit, dans le domaine des fréquences, par une convolution du spectre du signal et de la transformée de Fourier de la porte qui est un sinus cardinal. Cela provoque l'apparition d'ondulations (appelés lobes ou "pieds") de chaque coté des pics de cette transformée. L'échantillonnage de la transformée fait que ces lobes ne sont pas toujours visibles ou peuvent se traduire seulement par un élargissement très important de la base des pics. Ces lobes ont l'inconvénient de cacher des détails du spectre au voisinage des pics de forte amplitude. Pour les réduire, on remplace la multiplication par une porte par une multiplication par une autre fonction. Cette fonction "d'apodisation" est choisie de façon à ce que sa transformée de Fourier présente des ondulations faibles, ce qui aura obligatoirement pour inconvénient d'élargir la largeur des pics. On choisira cette fonction selon les besoins en précision et en sélectivité.
L'effet secondaire de l'apodisation est l'élargissement des pics qui dégrade la sélectivité. On considérera généralement cela comme un défaut et, dans le choix de la fonction d'apodisation, on réalisera un compromis entre l'atténuation souhaitée des lobes secondaires et cet élargissement. Cet élargissement peut pourtant être vu comme un avantage. En effet, on ne calcule que des échantillons de la transformée de Fourier. On peut considérer chaque point comme la sortie d'un filtre dont la réponse en fréquence a la forme de la transformée de Fourier de la fonction d'apodisation. En général une raie placée entre deux filtres donnera une amplitude plus faible qu'une raie centrée sur un filtre. Pour minimiser cette erreur, l'élargissement du filtre est favorable, l'idéal étant d'avoir un filtre dont la réponse est plate sur le sommet ("max-flat").
Réalisation MUSTIG
Observons le module de la transformée de Fourier d'un signal formé de la somme de 3 sinusoïdes de mêmes amplitudes et d'une quatrième de plus faible amplitude. Nous observons diverses formes de pics suivant la position des fréquences par rapport aux points d'échantillonnage de ce spectre. La raie de faible amplitude est pratiquement invisible.
![]()
Pour mieux visualiser le phénomène, on peut interpoler ce spectre. Pour cela on ajoute des "0" à la tranche de signal. Le module partie réalise cela (voir les explications de l'exemple "interpolation par TFD")

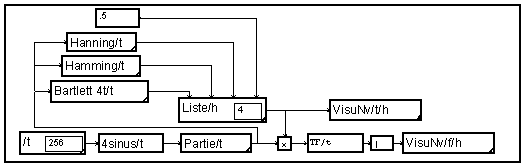
Quelques fonctions d'apodisation classiques sont disponibles en bibliothèque. Il faut, bien sûr, placer la fonction choisie sur une variable support de mêmes caractéristiques que le signal. On pourrait pour cela utiliser le graphe suivant :
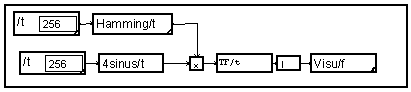
Mais ce graphe est peu commode à réutiliser puisqu'il nécessite de redéfinir toutes les caractéristiques de "t". Il est bien plus simple de réutiliser le support existant du signal pour la fonction d'apodisation :

Cette façon de procéder permet la réalisation d'une macro "Apodisation" d'usage général.


Cette macro d'apodisation pourra ainsi être réutilisée dans d'autres situations, y compris pour l'apodisation spatiale de signaux spatio-temporels d'antenne.
Il est par ailleur possible de faire une essai comparatif des actions de diférentes fenêtre, on ramplaçant la fenêtred'apodisation par une liste de fenêtre. La macro "VisuNv" permet de visualiser un une fois l'ensembe des courbes.