Utilisation de la TFD

Contenu

Transformée de Fourier Discrète de signaux complexes et réels. Modification des caractéristiques de la variable support. Transformée Inverse.

Mots clés

transformée de Fourier,  Fourier,  TFD, FFT,.

Fichiers MUSTIG associés

tf_discr.MTG

Exemples commentés voisins

Apodisation, Interpolation, Analyse spectrale.

Principes théoriques

Définitions

La transformée de Fourier Discrète (TFD)d'une suite discrète x(n) de N valeurs (que l'on pourra supposer périodique) est une suite discrète X(k) de N valeurs (que l'on pourra également supposer périodique) définie par les équations

 et

Le plus souvent, on utilisera cette transformée Discrète pour obtenir N valeurs de la transformée de Fourier continue (appelée "transformée en fréquence réduite"). Cette transformée est une fonction  X(l) périodique de période "1".

Un intérêt important de la TDF est l'existence d'algorithmes de calcul (FFT) de cette transformée beaucoup plus rapides qu'un calcul par application directe de la formule de base. Ces algorithmes imposent par contre des contraintes sur les  nombres de valeurs des signaux qui doivent généralement être des puissances de "2".

Application aux signaux continus

Sachant que souvent, un signal discret est issu de l'échantillonnage d'un signal continu à la fréquence f_e (et donc un pas =1/f_e)  :

x(n) = x(t) pour t=n/f_e

On utilise alors la TFD pour calculer (en général avec une approximation) des valeurs de la transformée de Fourier X(f) du signal continu. Dans ce cas la fréquence réduite l représente le rapport de la fréquence f à la fréquence d'échantillonnage f_e du signal. X(l) est donc considéré en pratique dans l'intervalle  [-0.5, +0.5] ou elle correspond à [-f_e/2, f_e/2]. Du fait de la périodicité de   X(l), l'intervalle des fréquences négatives [-0.5, 0] est identique à l'intervalle [0.5, 1]. On trouvera donc les valeurs correspondantes à ces fréquences négatives dans les points   N/2 à N-1 de la TFD.

On obtient donc N valeurs de la transformée de Fourier sur un intervalle f_e. C'est à dire un échantillonnage de cette transformée avec un pas de f_e/N.

Symétries

Si le x(t) est réel, X(k) possède une propriété de symétrie

X(k) =X^*(N-k)

^{Donc X(k) est entièrement représenté par l'intervalle [0, N/2], soit N/2+1 valeurs (complexes).} 

Augmentation du nombre de points

On pourra souhaiter un pas d'échantillonnage fréquentiel plus fin que f_e/N. Pour cela (on supposant le nombre de point (N) du signal imposé), il suffit d'augmenter artificiellement à M le nombre de points du signal en le prolongeant par des valeurs nulles. On obtient alors un pas d'échantillonnage de f_e/M. Cela revient à réaliser une interpolation de la transformée de Fourier et n'apporte bien entendu aucune information supplémentaire. Dans le cas ou le signal est une partie d'un signal long, cela mettra en évidence des oscillations qui pourront être atténuées par apodisation.

Réalisation MUSTIG

Transformée de Fourier de signaux élémentaires

Signal réel

Observons la TFD d'une portion de sinusoïde, fonction de la variable "t". Le modue "TF" de MUSTIG calcul en fait la TFD. Il fournit la transformée comme un signal fonction de la nouvelle variable "f". Ce signal est de type complexe, donc pour le visualiser, on peut utiliser la macro "Visu C" qui superpose les tracé des parties réelle et imaginaire, ou tracer séparément celles-ci, ou bien tracer le module.

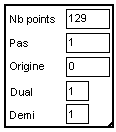
Par défaut, le pas d'échantillonnage des variables MUSTIG  est "1 seconde", et la fréquence d'échantillonnage est donc de "1 herz" (En fait, cela pourrait aussi bien être 1 mS et 1 KHz). Dans le cas le transformée de Fourier Discrète nous donne N (ici 256) valeurs de 0 à 1Hz. On peut vérifier à l'aide de la macro "Var?/f" que MUSTIG a correctement fixé le pas d'échantillonnage de "f" à 0.0039 c'est à dire 1/256. En fait, puisque le signal temporel est réel MUSTIG utilise la symétrie et le module "TF" ne donne ici que 129 valeurs correspondant au fréquences positives de 0 à 0.5Hz. On peut voir, avec la macro "Var?/f" l'indication "demi=1" qui mémorise cela.

On remplaçant la macro  par la macro  on peut facilement modifier la valeur du pas d'échantillonnage temporel du signal et observer comment évolue le pas d'échantillonnage en fréquence. Attention alors : la macro "Sinus" tient compte du pas d'échantillonnage. Il convient donc d'indiquer une fréquence exprimée en Hertz, et non pas une fréquence réduite.

On peut voir également avec la macro "Var?/f" l'indication "dual=1" qui mémorise le passage du temps  à la fréquence.

Signal complexe

On peut observer les propriétés de symétrie en donnant au signal le type complexe (Cela ne change pas les valeurs qui restent réelles).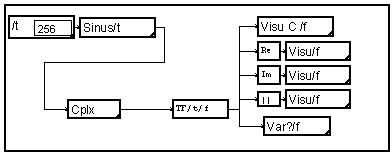

Dans ce cas MUSTIG ne tient pas compte de la symétrie et affiche la totalité de la transformée. On peut voir alors que dans les caractéristiques de "f",  demi=0.

Interpolation de la Transformée de Fourier

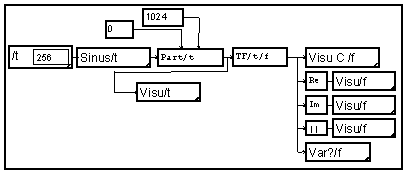
Pour augmenter le nombre des points du spectre, il suffit d'ajouter des valeurs nulles au signal. Cela est fait par le module "Part/t" ou par la macro "Partie/t", en précisant une nouvelle longueur (ici 1024) supérieure à la longueur initiale (256). Notons que l'on pourrait ajouter ces valeurs nulles au début, en donnant une origine négative.

Transformée de Fourier inverse

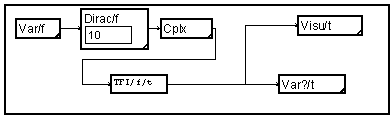
L'opération de transformée inverse est similaire. Par contre les propriétés de symétrie ne sont pas entièrement gérées. Le cas d'un signal réel en fréquence n'est pas pris en compte Au contraire, le type complexe est exigé. Par contre, l'indication "demi" est prise en compte.

   

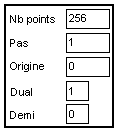
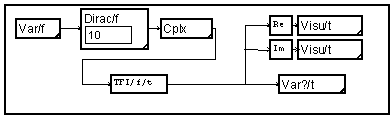
Le module "TFI" calcule la Transformée de Fourier Discrète Inverse. Le signal en fréquence. La macro "Var/f" définit les caractéristiques de "f". On met l'indication dual=1. Si demi-=0, on obtient après transformée un signal temporel complexe. Par contre si demi=1, on obtient un signal temporel réel. Attention dans ce cas à mettre une longueur de variable égale à une puissance de 2 plus un.