Convolution par TFD
Contenu
Convolution de deux signaux en utilisant la Transformée de Fourier Discrète (TDF). Cas des signaux courts : TFD globale. Cas des signaux long : TFD de blocs se recouvrant.
Mots clés
TFD, convolution, filtrage , calcul par blocs
Fichiers MUSTIG associés
Exemples commentés voisins
Utilisation de la TFD, filtrage RIF
Principes théoriques
Signaux courts
La convolution d'une suite 
par une suite
de durée
s'écrit
Cette équation de convolution est l'équation de base du
filtrage discret. Si 
est de longueur 
, 
est de longueur
. Pour réaliser rapidement cette convolution, on peut
profiter de l'efficacité de la TFD rapide. En effet, si 
est la Transformée de
Fourier Discrète (TFD) de 
et
la TFD de
, 
est la TFD de
(en notant
la convolution
circulaire).
Pour que le résultat de cette convolution circulaire soit le
même que celui d'une convolution simple, il faut prolonger chacun des signaux à
la longueur 
par des valeurs nulles.
Signaux longs ou infinis
Le calcul de la TFD est une opération globale sur tous les points du signal, ce qui n'est pas possible pour des signaux très long, et encore moins pour le traitement de signaux en temps réel (signaux infinis). Par contre, pour réaliser la convolution d'une signal long (ou même infini) par une signal de durée limité, ce qui correspond à un filtrage de type RIF, il est possible de découper le signal long en morceaux. Il convient alors de réunir correctement les morceaux, après avoir effectué des convolutions de chacun des morceaux. Il existe deux techniques.
La technique d'addition consiste à prolonger chaque morceau par des zéros pour réaliser des convolutions non circulaires, puis d'additionner les résultats dont le dates se chevauchent.
Le technique de juxtaposition consiste à prendre des morceaux qui se chevauchent sur une durée au moins égale à celle de la réponse impulsionnelle du filtre, et à ne conserver de chaque résultat que la partie qui ne comprend ni transitoire ni effet de circularité de la TDF.
Réalisation MUSTIG
Signaux courts
Le graphe suivant réalise la convolution circulaire de deux portes.
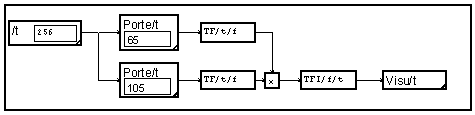
On peut observer le caractère circulaire de cette convolution en augmentant la longueur des portes sans augmenter le support (fixé ici à 256). On n'obtient plus alors un trapèze dont la base est à la valeur zéro. Pour ne pas être gêné par cette circularité, il faut augmenter la longueur du support des signaux. La macro ci-dessous réalise automatiquement cette opération : chacun des deux signaux est prolongé par des valeurs nulles à l'aide du module "part". La nouvelle longueur est fixée à la somme des deux longueurs. On effectue également un arrondi à la puissance de deux supérieure pour pouvoir utiliser la TFD rapide.
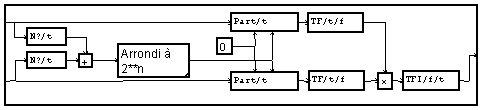
Cette macro ne fonctionne que si les pas d'échantillonnage des deux signaux d'entrée sont identiques. Or on utilise souvent la convolution pour réaliser un filtrage. Il sera alors nécessaire de forcer le pas d'échantillonnage de l'une des entrées à la valeur de l'autre. On peut ainsi réaliser une macro "filtrage" d'usage assez général. Notons que si le nombre de points des coefficients est faible devant celui du signal, on se contentera souvent d'une convolution circulaire, l'aspect circulaire étant limité au transitoire de faible durée ; cela évite d'augmenter inutilement le support du signal.
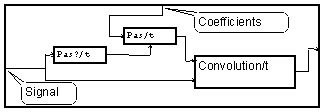
Signaux longs ou infinis
On présente la méthode de juxtaposition.
Supposons le signal déjà découpé en morceaux ou " blocs". Ce découpage peut être fait par une lecture d'un fichier par blocs (voir exemple....) ou par acquisition du signal (cas temps réel) bloc par bloc. Pour MUSTIG, cet ensemble de blocs sera un signal à deux dimensions : le temps à l'intérieur des blocs, et la date de chaque bloc. Dans l'exemple de test, le signal a une durée limitée et le découpage en blocs est fait artificiellement par le module "découpe". De même, pour visualiser le signal en une seule partie on utilise le module "recolle". On suppose dans cet exemple que la longueur de la réponse impulsionnelle du filtre est une puissance de 2.
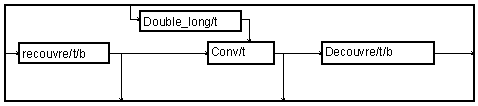
La macro "Double_long" prolonge la réponse impulsionnelle par des valeurs nulles. La Macro "recouvre" associe chaque bloc et son précédant pour former des blocs de longueurs doubles qui se recouvrent.
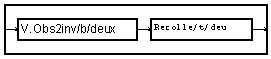
Pour cela, la macro "V.Obs2inv"
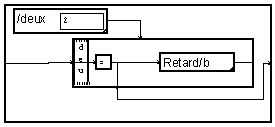
remplace chaque bloc par un vecteur de blocs (indicé par la variable "deux"). On pourra trouver une macro semblable pour la réalisation de filtres de type RIF : elle remplace alors chaque échantillon du signal par un vecteur glissant des dernières valeurs du signal. Ici, elle est utilisée selon la variable "b" qui indice les blocs, elle donne donc un vecteur de blocs, dont la longueur est fixée à deux. De plus, elle utilise un bouclage inverse[1], pour mettre le bloc le plus ancien en tête. (Noter la nécessité du module "=" dans ce cas, imposé par une restriction du compilateur MUSTIG). Les deux éléments de ce vecteur sont mis bout à bout par le module "recolle" pour former un bloc de longueur double.
La macro « convolution »
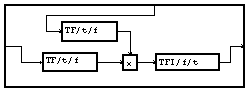
effectue la convolution (circulaire) de chaque bloc. Enfin, la macro "Decouvre"
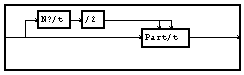
ne garde que la deuxième moitié des résultats.
On peut observer le fonctionnement de ces diverses opérations par la visualisation multicourbe "VisuNc".
Dans la macro "filtrage par petits morceaux" la réponse impulsionnelle est également découpée en petits blocs.
On pourra comparer le fonctionnement de ces deux macros à la convolution par une TFD globale, ainsi que par un filtrage de structure transversale.