Filtre à réponse impulsionnelle finie
Contenu
Différentes façons de décrire et de construire des filtres à réponse impulsionnelle finie (FIR). Forme diagramme de flux, forme vectorielle.
Mots clés
filtrage, RIF,FIR,,forme vectorielle,paquet
Fichiers MUSTIG associés
Exemples commentés voisins
Filtrage récursif, Convolution par TFD
Principes théoriques
Tout filtre discret est régi par une équation de convolution entre l'entrée et sa réponse impulsionnelle. Si un filtre discret possède une réponse impulsionnelle de longueur finie (RIF, ou FIR en anglais), cette convolution devient la façon la plus simple de mettre en oeuvre ce filtre :
![]()
Cette convolution, qui est aussi une équation aux différences
entre l'entrée ![]() et la sortie
et la sortie
![]() peut se représenter
sous forme d'un diagramme de flux qui comporte une ligne à retard et des
pondérations sur cette ligne. Cette forme est aussi appelée "filtre
transversal". Pour des raisons de parallélisme de calcul, on préfère
souvent une forme duale ou les retards sont placés entre les additions.
peut se représenter
sous forme d'un diagramme de flux qui comporte une ligne à retard et des
pondérations sur cette ligne. Cette forme est aussi appelée "filtre
transversal". Pour des raisons de parallélisme de calcul, on préfère
souvent une forme duale ou les retards sont placés entre les additions.
Pour accélérer le calcul, il est possible d'utiliser la transformée de Fourier discrète rapide. Voir exemple "convolution par TFD"
Réalisation MUSTIG
La description d'un filtre FIR par un diagramme de flux de forme directe ne présente pas de difficulté.

Pour dessiner rapidement cette structure répétitive, il est commode d'utiliser la commande MUSTIG "dupliquer". C'est pour cela que la cellule de base à été encadrée.
On peut de la même façon décrire un filtre sous sa forme duale.

On vérifiera que les sorties des filtres de ces deux formes sont identiques, à un retard près dû au retard inutile de la dernière cellule de la structure duale.
Le dessin du filtre sous sa forme développée n'est en pratique pas utilisable pour des filtres d'ordre supérieurs à quelques unités. Un "paquet " MUSTIG permet de ne dessiner qu'une seule cellule de base. On obtient ainsi une forme compacte de chacune des formes de diagramme.
![]()

![]()

La borne d'entrée du bord supérieur du paquet correspond à l'ensemble des coefficients de chaque cellule. Il faut y appliquer un signal fonction de la variable indice du paquet 'r'.
Ce peut être une simple constante vectoriel comme ci-dessous. Ce peut être la sortie d'un graphe qui calcule ces coefficients.

La démarche précédente non a amené naturellement à la création d'un paquet MUSTIG autour de l'ensemble de la cellule de base, en incluant le retard, le multiplieur et l'additionneur. En fait, on peut aussi bien faire des paquets séparés pour le retard et pour l'additionneur. La sortie du paquet contenant le retard est une fonction de deux variables le temps 't' et la variable indice du paquet 'r'. Pour qu'il existe un signal fonction de 'r' en entrée de ce paquet, il est nécessaire d'ajouter une borne reliée à l'entrée des coefficients. Le multiplieur n'a pas besoin de paquet : il bénéficiera des règles de bouclage implicite.

En compactant ces deux paquets en macros, on obtient une
forme "fonctionnelle" du filtre. La première macro fait correspondre
à chaque échantillon d'entrée ![]() un ensemble de
valeurs qui sont les échantillons d'entrée retardés
un ensemble de
valeurs qui sont les échantillons d'entrée retardés ![]() . Cet ensemble de valeurs peut s'interpréter comme un vecteur
glissant sur le signal.
. Cet ensemble de valeurs peut s'interpréter comme un vecteur
glissant sur le signal.
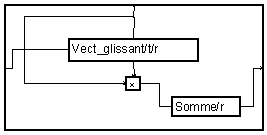
Le deuxième paquet est identique à la macro
"Somme" de la bibliothèque standard, appliquée selon la variable
"r". Si l'on considère également l'ensemble des coefficients du
filtre comme un vecteur, on voit que pour chaque échantillon de la sortie
![]() , on fait la somme des termes du vecteur glissant multipliés termes à termes par les
valeurs du vecteur de coefficients, c'est à dire un produit scalaire du vecteur
glissant et du vecteur des coefficients. On peut donc dessiner le filtre par le
graphe "vectoriel" suivant.
, on fait la somme des termes du vecteur glissant multipliés termes à termes par les
valeurs du vecteur de coefficients, c'est à dire un produit scalaire du vecteur
glissant et du vecteur des coefficients. On peut donc dessiner le filtre par le
graphe "vectoriel" suivant.
