Fenêtre glissante
Contenu
Application d'un traitement sur une fenêtre glissante sur le signal. Exemple en analyse spectrale évolutive.
Mots clés
fenêtre glissante, analyse spectrale, sonagramme, temps-fréquence, calcul par blocs
Fichiers MUSTIG associés
Exemples commentés voisins
Convolution par TFD, Analyse spectrale
Principes théoriques
Une mesure d'un paramètre d'un signal nécessite de disposer de ce signal sur une certaine durée, c'est à dire d'un certain nombre d'échantillons de ce signal. Si on cherche à mesurer un paramètre qui évolue, on souhaite faire des mesures successives. On peut pour cela découper le signal en tranches (ou "blocs") et appliquer la mesure sur chaque tranche. Cette technique présente l'inconvénient de lier la périodicité de la mesure à la durée de signal utilisée pour cette mesure. On souhaitera souvent obtenir plus de mesures. Pour cela, il faut utiliser des plages de mesures qui se recouvrent. On peut décrire cela par une fenêtre qui glisse sur le signal.
Un exemple typique d'application est l'analyse fréquentielle d'un signal non stationnaire pour réaliser une analyse "temps-fréquence". Le traitement le plus simple consiste en une analyse spectrale de chaque tranche, c'est-à-dire : apodisation, calcul de la transformation de Fourier (TFD) des échantillons de la fenêtre glissante puis du calcul du module. On peut réaliser seulement une analyse sur des tranches juxtaposées. On peut augmenter la cadence de mesure avec des tranches recouvrantes. La cadence maximale correspondrait à une estimation du spectre à chaque nouvel échantillon.
Réalisation MUSTIG
Le diagramme global de l'analyse se présente comme ci-dessous :
Nous ne décrirons ici que la macro "fenêtre glissante". La macro signal est dans l'exemple un ensemble de signaux modulés en fréquence. L'analyse est une analyse spectrale simple (voir exemple "Analyse spectrale").
Nous envisageons deux solutions pour réaliser la fenêtre glissante. La première utilise le module "partie". Elle permet de régler indépendamment la longueur de la fenêtre et son pas de décalage, mais n'est pas utilisable en mode temps réel (sur un signal de durée non limité). La seconde utilise le principe du vecteur glissant de bloc. Elle est plus contraignante pour le choix des paramètres, mais est généralisable au temps réel.
Utilisation du module "partie"
Une fenêtre étant une partie d'un signal, il parait naturel d'utiliser le module "partie/t" pour extraire cette fenêtre. Il suffit de calculer la suite des positions (rang des points du signal correspondant aux premiers points de la fenêtre). Si l'on tente cette expérience, on obtient un message d'erreur "Les définitions de variables doivent être statiques". En effet, le module partie présente la particularité (souvent appréciable) de mémoriser la position origine de la partie dans les caractéristiques de la variable support. Cette position ne doit donc pas être variable[1]. Il faut donc utiliser le module "Part_dec/t", qui fixe l'origine de la sortie à zéro.
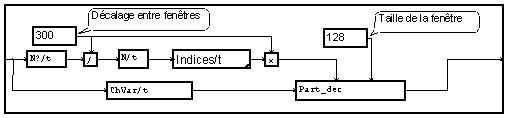
La suite des positions des fenêtres est une fonction de la nouvelle variable "t".(Pour pouvoir conserver le même nom de variable qu'en entrée, on a fait un changement de nom de variable du signal d'entrée de "t" à "tl"). La longueur de cette nouvelle variable est calculée par division du nombre de point du signal par la valeur du décalage entre deux fenêtres. Pour que graduation de l'axe du temps de la visualisation du diagramme temps-fréquence tienne compte des caractéristiques du signal, il faut fixer correctement le pas la variable nouvelle variable "t". On obtient le graphe ci-dessous.
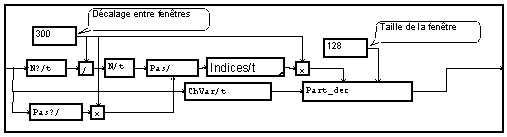
Notons que l'utilisation du module "partie" impose la mémorisation complète du signal. Cette technique n'est donc pas généralisable au fonctionnement temps-réel, avec un signal de durée non limité.
Utilisation de vecteur glissant
Une autre façon de décrire une fenêtre glissante est celle
utilisée pour la réalisation de filtre à réponse impulsionnelle finie. (Voir
exemples "Filtrage RIF"). A chaque point 
du signal, on associe l'ensemble 
des valeurs retardées
de ce signal. Nous avions construit ainsi une macro "vecteur
glissant". Une macro "Vect.gliss" identique est disponible en
bibliothèque en V4.
On peut construire un analyseur temps-fréquence en effectuant l'analyse spectrale de ce vecteur glissant pour chacun des points du signal.
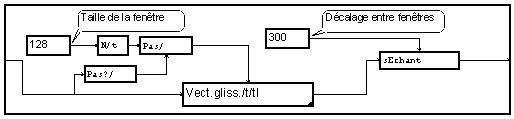
On ne souhaitera généralement pas effectuer cette analyse pour chacun des points. L'utilisation de "sous-échantillonne/t" avec un coefficient M permet de ne garder que un vecteur sur M. Cette solution n'est pas très efficace : elle est relativement lente, car le compilateur MUSTIG ne sait pas simplifier le "glissement" de la fenêtre pour tenir compte de la présence du sous-échantillonnage placé en aval. Elle est également gourmande en mémoire, car le module de sous-échantillonnage de MUSTIG exige actuellement que son signal d'entrée soit entièrement en mémoire. Cette solution ne sera donc souvent pas applicable en pratique, en particulier en temps réel.
Utilisation de vecteur glissant de blocs
Pour obtenir une solution plus efficace, il faut partir d'un signal préalablement découpé en blocs. Le découpage préalable sera souvent fait à l'extérieur du traitement, au moment de la lecture d'un fichier ou de l'acquisition du signal. Le fonctionnement temps réel est alors possible. Dans cet exemple de test, le signal a une durée limitée et le découpage en blocs est fait artificiellement par le module "découpe" (précédé d'un changement de nom de variable par commodité). La macro "Vect.gliss.Inv" appliquée à une suite de blocs donne un vecteur glissant dont les éléments sont des blocs. (La macro "Vect.gliss" classe les éléments du plus récent au plus ancien. Il est nécessaire de faire le contraire.) Le module "recolle" juxtapose les blocs entre eux pour obtenir la fenêtre d'analyse glissante. Le décalage entre les fenêtres est égal à la taille des blocs initiaux.
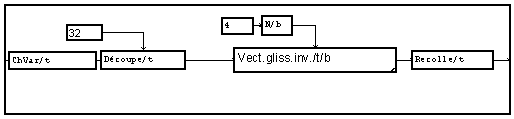
Notons que dans l'exemples "convolution par TFD", un opération analogue est réalisée, avec un recouvrement fixe de moitié des blocs.