Analyse spectrale
Contenu
Analyse spectrale d'un signal par Transformée de Fourier Discrète : méthode du spectrogramme, méthode du corrélogramme.
Mots clés
analyse spectrale
Fichiers MUSTIG associés
Exemples commentés voisins
Utilisation de la TFD, apodisation, Fenêtre glissante
Principes théoriques
L'analyse spectrale de base consiste simplement en une TFD (transformées de Fourier discrète), éventuellement suivie du calcul du module. On se référera à l'exemple "TFD bases". Si ce signal est en fait une portion d'un signal infini, il sera généralement utile d'apodiser le spectre en multipliant le signal par une fenêtre de pondération. Voir l'exemple "apodisation".
Si le signal est aléatoire, il est nécessaire d'effectuer un moyennage du spectre. La technique la plus classique consiste à effectuer un certain nombre de transformées de Fourier de parties de ce signal, et d'en calculer la moyenne quadratique. La plus simple pour cela est de découper le signal en blocs juxtaposés. On obtiendra un meilleur résultat en prenant des blocs qui se recouvrent partiellement. La résolution obtenue (le pas d'échantillonnage en fréquence) est fixée par la taille des TFDs (et donc des blocs). La variance du résultat sera d'autant meilleur que le nombre de blocs moyenné sera grand. Pour un signal de durée donné, il faudra donc régler le compromis entre ces deux objectifs.
Une autre technique est d'effectuer un lissage du spectre. Ce lissage revient à un filtre passe-bas complété éventuellement d'un sous-échantilonnage. Il peut être effectué sur la transformée de Fourier inverse de ce spectre (qui est la fonction d'autocorrélation du signal), par multiplication par une fonction appropriée.
Si le signal n'est pas stationnaire il faut utiliser une méthode d'analyse de type "temps-fréquence". Le plus simple est d'effectuer une analyse sur une fenêtre glissante sur le signal. Voir exemple "Fenêtre glissante".
Réalisation MUSTIG
Signal certain fini
Voir exemples "TFD bases" et "apodisation".
Signal aléatoire
Nous utilisons comme signal test un bruit filtré.

Le filtre est la cascade de cellules de deuxième ordre étudié dans l'exemple "filtre récursif". C'est un filtre passe-bas. On peut vérifier qu'une simple TF ne donne pas un résultat satisfaisant.
Spectrogramme
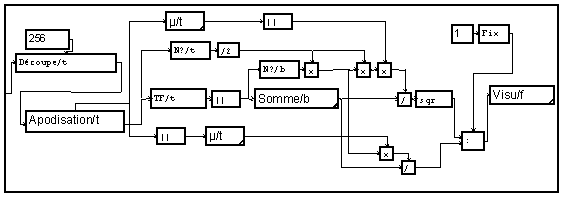
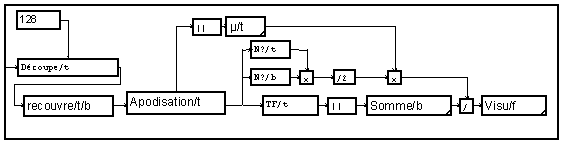
Le module "decoupe/t/b" découpe le signal en blocs jointifs. Sa sortie est un signal MUSTIG dépendant de deux variables : "t" est le temps dans chaque bloc et "b" est l'indice des blocs. Le module "TF/t/f" réalise la TFD de tous les blocs. En sortie, le signal est une fonction de la variable "f" et de la variable "b". La somme des spectres entre eux est faite par la macro "Somme".
Cet analyseur effectue une mesure de la densité spectrale d'énergie du signal intégré sur toute sa durée. Pour tenir compte de la puissance des fréquences négatives non visualisées, on appliquera un facteur deux.
Souvent, on ne dispose que d'une partie d'un signal considéré comme infini et on préférera obtenir une densité spectrale d'énergie (exprimée en volts carrés par hertz). Pour cela, il suffit de diviser le résultat précédent par le nombre de points du signal. En fait, le découpage du signal en blocs sera souvent fait à l'extérieur de traitement (par le module d'acquisition ou le module de lecture d'un fichier). Il est donc préférable de retrouver ce nombre de points en faisant le produit de nombre de points par tranches (obtenu par "N?/t") par le nombre de tranches (obtenu par "N?/b"). Pour tenir compte de la puissance des fréquences négatives non visualisées, on applique un facteur deux.
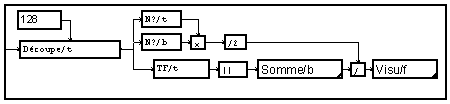
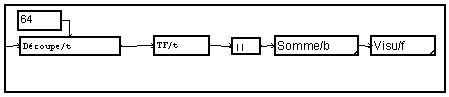
On peut vérifier que si on multiplie la densité spectrale obtenue par la largeur de bande, on retrouve bien la mesure de la puissance moyenne du signal.
Il pourra être utile d'ajouter une multiplication par une fenêtre de pondération pour réaliser une bonne apodisation du spectre.
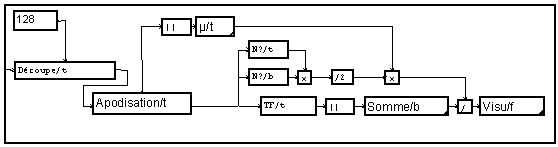
Il faut alors corriger l'amplitude de la densité spectrale pour tenir compte de cette fonction de pondération. La solution utilisée, qui fonctionnera pour toute fonction, est de diviser par la moyenne du carré de la fonction.
Pour faire l'analyse sur des blocs qui se recouvrent, il suffit d'ajouter la macro "recouvre/t/b" (Voir sa description dans l'exemple "convolution par TFD").
Corrélogramme
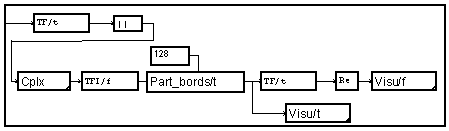
On calcule tout d'abord le spectre global par les modules
"TF" et ![]() (module carré). Pour
obtenir la fonction de corrélation, il faut calculer la transformée de Fourier
inverse de ce spectre. Si l'on applique directement le module
"TFI/f/t", on obtient un message d'erreur. En effet, d'une part le
spectre possède un support de type "demi", puisque le signal analysé
est réel (voir exemple "TF bases"). D'autre part, le module
(module carré). Pour
obtenir la fonction de corrélation, il faut calculer la transformée de Fourier
inverse de ce spectre. Si l'on applique directement le module
"TFI/f/t", on obtient un message d'erreur. En effet, d'une part le
spectre possède un support de type "demi", puisque le signal analysé
est réel (voir exemple "TF bases"). D'autre part, le module ![]() a rendu un signal
réel. Or il se trouve que cette combinaison n'est pas gérée par MUSTIG dans la
version actuelle. Pour y remédier, il suffit, soit de donner à nouveau au
spectre le type complexe (bien que ses valeurs soient réelles), soit de
remplacer le module
a rendu un signal
réel. Or il se trouve que cette combinaison n'est pas gérée par MUSTIG dans la
version actuelle. Pour y remédier, il suffit, soit de donner à nouveau au
spectre le type complexe (bien que ses valeurs soient réelles), soit de
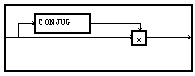
remplacer le module ![]() par la macro
ci-dessous.
par la macro
ci-dessous.
La fonction d'autocorrélation possède des valeurs importantes autour de t=0. Seules ces valeurs sont utiles. Mais le caractère cyclique de la TFD fait que ces valeurs se retrouvent au début et à la fin. La macro "Part_bord"
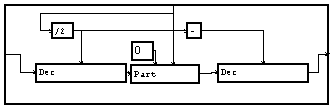
se charge de ne garder que ces parties. Une dernière TFD nous donne le spectre lissé. Ce spectre est de type complexe, bien qu'il ne soit composé que de valeurs réelles. On ne garde donc que la partie réelle.
Notons qu'il pourra être utile d'ajouter une multiplication par une fenêtre de pondération avant la dernière TF pour réaliser une bonne apodisation du spectre.
Comme dans le spectrogramme, il faut diviser le résultat par le nombre de points pour obtenir une densité spectrale de puissance moyenne.
Signal composé de fréquences pures
Spectrogramme
Si on s'intéresse à principalement à des fréquences pures, qui se traduisent dans le spectre par des raies, on souhaite généralement mesurer l'amplitude de ces composantes, exprimée en volt. La variante suivante du spectrogramme réalise cette fonction.

Le résultat des transformées de Fourier est divisé par le nombre de points du bloc, ce qui donne des spectres d'amplitude souhaitée. Ensuite, la somme des spectres est divisée par le nombre de blocs, pour obtenir une valeur moyenne. On notera que cela n'est pas équivalent à la division globale par le nombre de points, puisque l'une des divisions porte sur les amplitudes et l'autre sur des amplitudes au carré. La simplification suivante est possible.

On peut facilement combiner cette structure avec celle du spectrogramme dont la sortie est en "volts carrés par hertz" pour pouvoir commuter facilement d'un mode à l'autre.
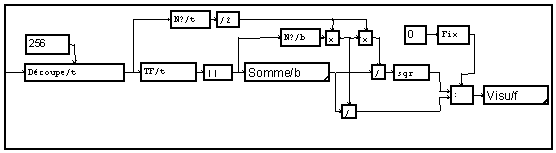
Si on complète le traitement par une apodisation, il faut corriger l'amplitude. Il faut, pour la mesure d'amplitudes de raies, diviser les amplitudes par la moyenne de la fonction utilisée. Le graphe suivant correspond à un analyseur avec apodisation commutable du mode "volts carrés par hertz" au mode "volts".