Filtrage récursif
Contenu
Réalisation de filtres définis par une équation aux différences au par un diagramme de flux. Filtres du premier ordre, cellules du second ordre, cascade de cellules du second ordre. Utilisation sur une suite de blocs.
Mots clés
filtrage, diagramme de flux,calcul par blocs
Fichiers MUSTIG associés
Exemples commentés voisins
filtrage transversal, filtrage par TFD
Principes théoriques
De façon générale, un filtre discret linéaire peut être
défini par une équation aux différences finies liant l'entrée du filtre![]() et sa sortie
et sa sortie![]() .
.
![]()
Dans le cas particulier où tous les coefficients ![]() (pour
(pour
![]() ) sont nuls , la réponse impulsionnelle du filtre
) sont nuls , la réponse impulsionnelle du filtre
![]() est de durée finie et
est de durée finie et
![]() . On qualifie alors le filtre de filtre à Réponse
Impulsionnelle Finie (RIF).
. On qualifie alors le filtre de filtre à Réponse
Impulsionnelle Finie (RIF).
Dans les autres cas, on le qualifie de filtre à Réponse Impulsionnelle Infinie (RII). L'échantillon du signal de sortie de rang n étant fonction des échantillons précédents (de rang n-1, n-2...) du même signal, on qualifie souvent ce type de filtre de "filtre récursif".
On peut remplacer l'écriture de l'équation aux différences par un graphe composé d'opérateurs "addition", "gain" et "retard". On appelle ce graphe un "diagramme de flux". Ce graphe peut servir à l'implémentation physique du filtre.
Par transformation en "Z" de l'équation aux
différences, on fait apparaître la fonction de transfert du filtre, qui est la
transformée en "Z" de la
réponse impulsionnelle du filtre ![]() . La factorisation de cette fonction de transfert met en
évidence ses pôles et les zéros, qui peuvent notamment renseigner sur la
stabilité du filtre. Cette factorisation permet de mettre l'expression de la
fonction de transfert sous la forme d'un produit de termes d'ordre deux. Chacun
d'eux correspond à un filtre d'ordre deux, dont l'équation aux différences sera
:
. La factorisation de cette fonction de transfert met en
évidence ses pôles et les zéros, qui peuvent notamment renseigner sur la
stabilité du filtre. Cette factorisation permet de mettre l'expression de la
fonction de transfert sous la forme d'un produit de termes d'ordre deux. Chacun
d'eux correspond à un filtre d'ordre deux, dont l'équation aux différences sera
:
![]()
ou une forme normalisée avec ![]() et
et
![]() :
:
![]()
Si ce filtre est à
coefficients réels, ses pôles et zéros sont complexes conjugués. En notant ![]() l'un de pôles et
l'un de pôles et
![]() l'un des zéros, les
coefficients de la cellule du second ordre sont :
l'un des zéros, les
coefficients de la cellule du second ordre sont :

Réalisation MUSTIG
Filtre récursif du premier ordre
L'équation aux différences finies la plus simple de ce filtre, s'écrit :
![]()
On peut calculer cette équation par une itération :
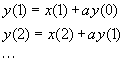
Cette itération est réalisée par le graphe MUSTIG :

Notons que ![]() est préalablement
initialisée à une valeur arbitrairement fixée à zéro.
est préalablement
initialisée à une valeur arbitrairement fixée à zéro.
Cette forme de graphe, simple pour un filtre du premier ordre, deviendrait très lourde pour un ordre élevé. Il sera généralement plus facile d'utiliser un graphe de type "diagramme de flux".
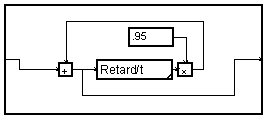
Sous cette forme, la valeur initiale ![]() n'est pas visible,
car c'est la valeur initiale du "retard". Il est éventuellement
possible de modifier cette macro pour changer cette valeur initiale. Dans
certains cas, il pourra également être nécessaire de modifier le type de cette
valeur initiale.
n'est pas visible,
car c'est la valeur initiale du "retard". Il est éventuellement
possible de modifier cette macro pour changer cette valeur initiale. Dans
certains cas, il pourra également être nécessaire de modifier le type de cette
valeur initiale.
Notons que les deux formes précédentes du filtre sont totalement équivalentes pour le compilateur MUSTIG qui générera exactement le même code de calcul dans les deux cas (voir paragraphe 2-6 du manuel d'utilisation pour des explications plus précises).
Filtre du deuxième ordre
On utilise l'une des formes de diagramme de flux de la
cellule de filtre d'ordre deux, avec le coefficient ![]() . Sa réalisation MUSTIG revient au simple dessin de ce
diagramme de flux.
. Sa réalisation MUSTIG revient au simple dessin de ce
diagramme de flux.

On peut faciliter le dessin de tels diagrammes à coefficients fixes en utilisant une macro "gain" :
![]()
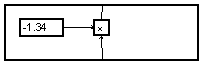
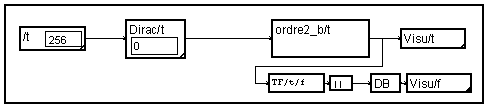
Pour vérifier le fonctionnement de ce filtre, on peut observer sa réponse impulsionnelle en lui injectant un "Dirac". La transformée de Fourier de cette réponse impulsionnelle donne la réponse en fréquence.
Filtre du deuxième ordre défini par ses pôles et zéros
Si l'on préfère définir le filtre par les valeurs (complexes) de ses pôles et de ses zéros, on ajoute la macro
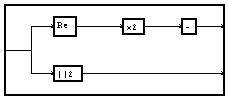
qui calcule les coefficients a ou b à partir des zéros ou des pôles

Nous utilisons la macro "pole et zéros" pour définir graphiquement la position de ceux-ci dans le plan complexe (voir ???? pour la description de cette macro)
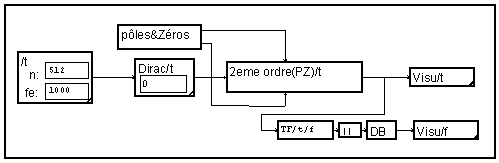
Cascade de cellules Filtre du deuxième ordre
Pour réaliser une cascade de filtres, on peut, bien entendu, placer plusieurs macros "ordre_2" en cascade. Il sera alors commode de mettre les coefficients en image sur la macro pour pouvoir les éditer facilement.
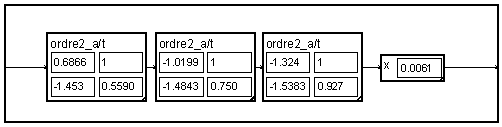
On peut éviter la duplication des cellules et n'en dessiner qu'une seule mise dans un "paquet". Pour cela, il faudra remplacer les coefficients scalaires par des fonctions de la variable de boucle. Il est plus simple pour cela d'utiliser la macro "2eme ordre(PZ)" dont les entrées sont les valeurs complexes d'un des pôles conjugués et d'un des zéros conjugués. On forme une liste de valeurs de pôles fonction de la variable "ordre". On fait de même pour les zéros.

Filtrage récursif d'une suite de blocs
Pour appliquer un filtre récursif sur un signal long enregistré sur un fichier disque, il serait possible de lire et d'écrire les valeurs une par une (Voir exemples "lecture enregistrement fichiers"). Cela risque d'être trop lent. D'autre part, on peut avoir besoin de faire cohabiter des traitements d'analyse spectrale, fonctionnant par blocs, avec des filtrages récursifs.
Si l'on applique sans modification un signal découpé en blocs à un filtre récursif, chacun des blocs va être filtré indépendamment des autres avec un filtre réinitialisé au début de chaque bloc. Pour obtenir un filtrage continu, il faut que l'état initial du filtre d'un bloc soit l'état final du filtre du bloc précédent. Dans la forme diagramme de flux, l'état du filtre est contenu dans les retards. Il suffit donc de reboucler l'état final d'un retard sur son entrée à l'aide d'un paquet MUSTIG indicé par la variable indice des blocs. Cela se fait en remplaçant dans le filtre tous les "retard/t" par la macro "retard/t/b".
