Filtrage Multi-cadence
Contenu
Filtrage avec changement de fréquence d'échantillonnage
Mots clés
interpolation, sous-échantillonnage, décimation, suréchantillonnage, filtrage, multicadence
Fichiers MUSTIG associés
Exemples commentés voisins
interpolation, interpolation par TFD
Principes théoriques
Décimation par un facteur entier
La réduction de fréquence d'échantillonnage est souvent appelée "décimation". Si le rapport de réduction est un nombre entier "k", cette opération revient à ne garder qu'un échantillons sur k. Mais pour être certain de respecter les conditions d'échantillonnage de Schannon, il convient d'effectuer préalablement un filtrage passe-bas (pour la même raison, il convient de placer un filtre passe-bas "anti-repliement" sur un signal continu avant son échantillonnage). Si ce filtre passe-bas est réalisé par un filtre à réponse impulsionnelle finie de type transversal, la décimation est réalisée par le schéma suivant :
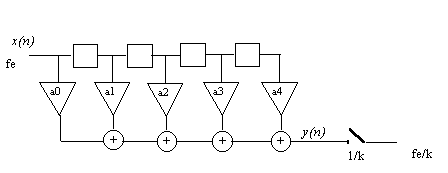
En fait, il est inutile de calculer les échantillons de sorties non utilisés :
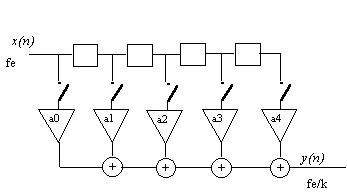
Cette structure est plus économique en calcul.
Interpolateur facteur entier
L'augmentation de la fréquence d'échantillonnage dans un rapport entier "p" peut se faire par insertion de k-1 valeurs nulles après chaque échantillon, puis d'un filtrage passe-bas pour supprimer les spectres dupliqués:
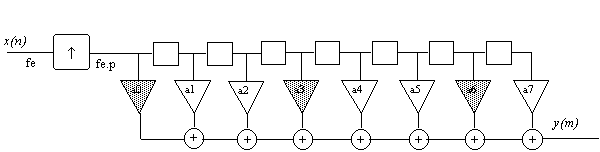
En fait, on constate que seuls 1/p des multiplieurs du filtre transversal opèrent sur des données non nulles. Il est plus économique en calcul de considérer que à chaque échantillon correspondent successivement les différentes sorties de p filtres opérant sur les échantillons d'entrée. On obtient une structure connue sous le nom de filtre polyphase.
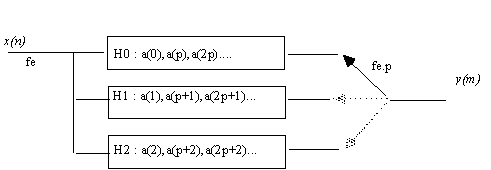
Les R.I. des filtres Hi sont obtenus par des échantillonnages décalés de la R.I du passe bas fonctionnant à la fréquence d'échantillonnage haute.
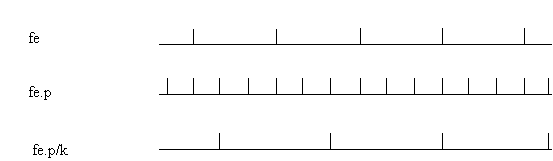
Décimateur facteur fractionnaire
Pour passer de la fréquence d'échantillonnage fe à la fréquence d'échantillonnage fe.(p/k), on pourrait faire tout d'abord une augmentation de la fréquence pour obtenir fe.p, puis une décimation dans un rapport k. Il n'est pas nécessaire d'ajouter un passe-bas avant la décimation puisqu'il existe déjà celui de l'interpolateur. Il suffit donc de sous-échantillonner la sortie du filtre polyphase précèdent.
En fait, il n'est pas nécessaire de calculer les filtres dont les sorties sont inutilisées. Le filtre peut alors se décrire par le digramme suivant :
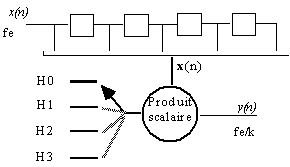
Il est possible d'utiliser cette structure dans le cas d'un rythme de sortie quelconque, en approximant l'échantillon de sortie à la valeur à l'horloge fe.p la plus proche.
Réalisation MUSTIG
Les exemples de réalisation présentés ici utilisent les opérateurs de sous-échantillonnage vectoriels disponibles en MUSTIG 4.1. Cela restreint leur utilisation à des signaux de longueur limitée ou découpés en blocs. Dans les versions ultérieures, des opérateurs scalaires permettront un fonctionnement temps réel plus complet.
Décimation par un facteur entier
En décrivant le filtre transversal à l'aide d'une macro "Vecteur glissant" et d'une macro "produit scalaire", on obtient le schéma de départ :
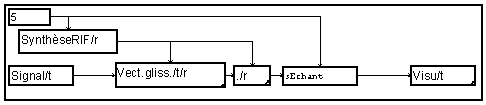
On vérifie qu'il est équivalent (mais plus rapide !) de placer le module de sous-échantillonnage avant le produit scalaire.
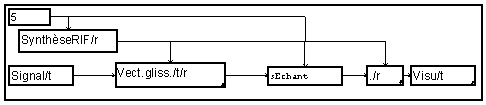
La macro "Synthèse RIF" calcule les coefficients d'un filtre passe-bas en fonction du rapport de sous-échantillonnage fourni en paramètre.
Interpolation par un facteur entier
On peut facilement vérifier le fonctionnement de la méthode élémentaire : insertion de zéros et filtrage. L'insertion de valeur nulle est réalisée par la macro "Suréchantillonne_0" (voir exemple commenté "Interpolation"). L'amplitude du signal est multipliée par le facteur "p" de suréchantillonnage pour conserver la puissance du signal.
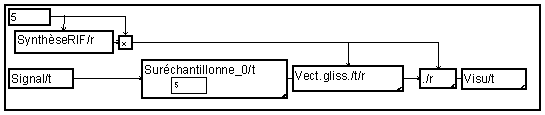
Pour transformer ce graphe en un filtre polyphase, on décompose la réponse impulsionnelle en un ensemble de p réponse par la macro "Demultiplex".
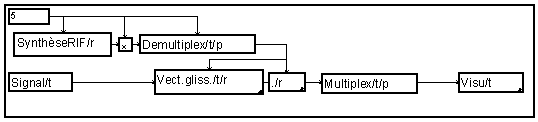
En sortie du filtre, on a donc un ensemble de signaux qu'il suffit de multiplexer pour obtenir le signal sur-échantillonné.
Décimation par un facteur fractionnaire
Nous supposons que nous réalisons bien une réduction de fréquence d'échantillonnage, c'est à dire que le rapport k/p est inférieur à 1. Dans ce cas, nous avons au plus un échantillon de sortie dans chaque période du signal d'entrée.
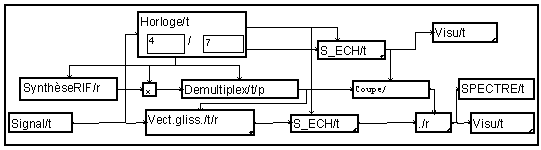
La macro "Horloge" élabore un signal logique qui indique s'il y a un échantillon de sortie correspondant à l'échantillon d'entrée. Ce signal est appliqué comme signal de validation à la macro "S_ECH". Celle-ci ne laisse passer que les échantillons valides. La macro "Horloge" calcule en plus la position de l'échantillon de sortie relative à l'échantillon de sortie. Cette position est utilisée pour choisir, par le module "coupe", le jeu de coefficients à utiliser pour calculer cet échantillon.
En utilisant cette même macro "horloge", on peut facilement réaliser des changeurs de fréquence sans interpolation ou avec une simple interpolation linéaire. On observant les spectres des signaux de sortie, on constate que ces structures simples présentent des lobes parasites, alors que la structure avec interpolation par filtre polyphase n'en présente pas.